Перенос данных из других задач

ELCUT позволяет переносить источники поля (распределенные нагрузки), рассчитанные в одной задаче, в задачи другого типа. Предусмотрены следующие типы связи между задачами:

• Поле температур, обусловленное джоулевыми (омическими) потерями. Потери могут вычисляться в задачах электрического поля постоянных или переменных токов, а также в задачах расчета магнитного поля с учетом вихревых токов.
• Анализ механических напряжений с учетом рассчитанного распределения температуры.
• Расчет механических напряжений, вызванных магнитными силами.
• Расчет механических напряжений, вызванных электростатическими силами.
• Запоминание магнитного состояния вещества для использования в последующих, линеаризованных задачах расчета магнитного поля.
• Расчет магнитного поля переменных токов с учетом зависимости электропроводности материалов от температуры.
• Особый вид связи задач, позволяющий импортировать решение одной задачи в качестве начального состояния для другой нестационарной задачи.

В связанной задаче, в дополнение к источникам (нагрузкам), перенесенным из другой задачи, могут быть заданы прочие источники, как в обычной задаче.

Есть возможность совместить разные типы связи в одной задаче. Например, после расчета растекания токов, электростатических и магнитных полей в разных задачах, использующих один и тот же файл геометрии модели, вы можете рассчитать распределение температуры, вызванное джоулевыми потерями, а затем - механические напряжения, вызванные действием температурных деформаций, электростатической и магнитной силой одновременно. К счастью, такие задачи весьма редки на практике.

В дальнейшем изложении назовем задачу, из которой переносятся данные - источником, а задачу, в которую переносятся данные - целевой задачей. ELCUT накладывает некоторые ограничения на связанные задачи:

• Как задача-источник, так и целевая задача должны использовать один и тот же файл геометрии модели.
• Обе задачи должны использовать одну и ту же систему координат (декартову или цилиндрическую).
• К моменту решения целевой задачи задача-источник должна быть решена.

Замечание. Несмотря на требование единого файла модели для обеих задач, их расчетная область может не совпадать, поскольку часть подобластей, используемая в одной задаче, может быть исключена из рассмотрения в другой.

Учёт джоулевых потерь в тепловой задаче

При переносе данных из задачи электрического поля постоянных токов в тепловую задачу, мощность тепловыделения (джоулевы потери) рассчитываются по закону Джоуля-Ленца. Они учитываются в каждой подобласти, включенной в рассмотрение в обеих задачах. При переносе данных из задачи магнитного поля переменных токов, джоулевы потери рассматриваются во всех проводящих областях.

Учёт распределения температур в задаче теории упругости

При расчете термических деформаций по полю температур, перенесенному из тепловой задачи, начальные деформации учитываются в каждой подобласти, включенной в рассмотрение в обеих задачах, если в подобласти задано ненулевое значение коэффициента теплового расширения (или хотя бы одной из его компонент в анизотропном случае).

Учёт магнитных сил в задаче механики

При переносе магнитных сил в задачу механики:

• Объемные силы учитываются во всех блоках, включенных в рассмотрение в обеих задачах, если подобласть обладает нелинейными магнитными свойствами, или в подобласти протекает ток (по закону Лоренца).
• Поверхностные силы учитываются на всех границах, разделяющих подобласти с разными магнитными свойствами, границах, несущих поверхностный ток, или внешних границах области (в смысле магнитной задачи). Поверхностная сила учитывается даже в том случае, если подобласть, к примеру, слева от границы исключена из рассмотрения в магнитной задаче, а подобласть справа - в механической.

Учёт электростатических сил в задаче теории упругости

При переносе электростатических сил в задачу теории упругости:

• Объемные силы учитываются во всех подобластях, включенных в рассмотрение в обеих задачах, если в подобласти задана плотность распределенного заряда;
• Поверхностные силы учитываются на всех границах, разделяющих подобласти с разной диэлектрической проницаемостью, границах, несущих поверхностный заряд или внешних границах области в смысле электростатической задачи. Поверхностная сила учитывается даже в том случае, если подобласть, к примеру, слева от границы исключена из рассмотрения в электростатической задаче, а подобласть справа - в механической.

Решая задачу магнитостатики с учетом насыщения материала, мы можем запомнить магнитное состояние вещества в задаче-источнике для использования в последующих целевых задачах (магнитостатики или магнитного поля переменных токов).
Объектом переноса является значение магнитной проницаемости вещества, вычисленное в каждом конечном элементе задачи-источника.

• В нелинейных материалах переносится значение магнитной проницаемости, вычисленное с учетом величины магнитного поля в задаче-источнике;
• В линейных материалах запоминается магнитная проницаемость, которая была задана в качестве свойств метки блока в задаче-источнике.

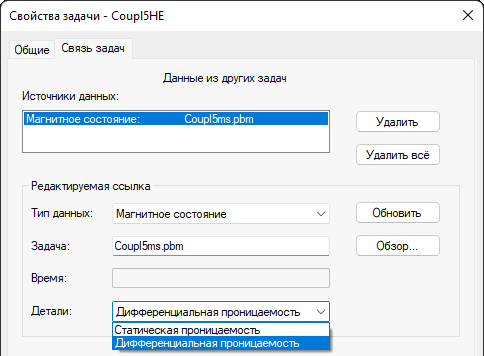
Учитывая, что существует два вида магнитной проницаемости - статическая и дифференциальная, диалог импорта имеет переключатель выбора нужного типа импортируемой характеристики. Следует отметить, что различные виды расчетов могут потребовать разных типов импортируемой магнитной проницаемости.

Рис. Диалоговое окно Связь задач.

Целевая задача становится линейной, то есть магнитная проницаемость вещества больше не зависит от рассчитанного магнитного поля.
Запоминание магнитного состояния равносильно фиксации рабочей точки магнитной системы. В результате фиксации появляется возможность определять в целевых задачах дифференциальные собственные и взаимные индуктивности многообмоточных систем, рассчитывая для каждой из обмоток магнитный поток, вызванный действием только одной из обмоток системы.

Учёт распределения температур в задаче магнитного поля переменных токов

Зависимость электропроводности материала от температуры может быть использована в задачах электрического поля постоянных токов, нестационарного магнитного поля и магнитного поля переменных токов.

Однако, только для задач магнитного поля переменных токов данные о температуре могут быть получены из решения тепловой задачи. В остальных задачах априорно известная температура для каждого блока задается константой или формулой от координат и времени.

См. также
Примеры задач ELCUT - Связанные (мультидисциплинарные) задачи