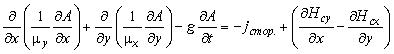 ,
,
Задача расчета нестационарного магнитного поля представляет собой общий случай расчета магнитного и электрического полей, вызванных переменными токами (синусоидальные, импульсные и др.), постоянными магнитами, или внешним магнитным полем, в линейной и нелинейной (ферромагнитной) среде, с учетом вихревых токов (поверхностный эффект).
Формулировка задачи может быть получена из уравнений Максвелла для векторного магнитного потенциала A (B = rot A, B - вектор магнитной индукции), и скалярного электрического потенциала U (E = -grad U, E - вектор напряженности электрического поля):
rot(μ-1·rot A) = j + rot Hc
j = γE = -γ·grad U - γ·∂A/∂t,
где μ-1 тензор, обратный тензору магнитной проницаемости, и γ - электропроводность.
В соответствии со вторым уравнением, полный ток в проводнике может рассматриваться как сумма стороннего тока, вызванного приложенным извне напряжением, и вихревого тока, индуцированного переменным магнитным полем
j = jстор + jвихр,
где
jстор = -γ·grad U
jвихр = -γ·∂A/∂t.
Если расчет поля проводится совместно с присоединенной электрической цепью, уравнение цепи, содержащей массивный проводник в магнитном поле записывается как:
I = U/R - ωγ· s∫A·dS ,
где
U - падение напряжения на массивном проводнике, и
R - активное сопротивление проводника на постоянном токе.
В рассматриваемых задачах вектор индукции B всегда лежит в плоскости модели (xy или zr), а вектор плотности тока j и векторный потенциал A перпендикулярны к ней. Отличны от нуля только компоненты jz и Az в плоско-параллельном случае или jθ и Aθ в осесимметричных задачах. Мы будем обозначать их просто как j и A. Для плоскопараллельных задач уравнение имеет вид:
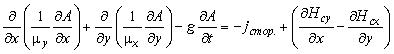 ,
,
а для осесимметричного случая:
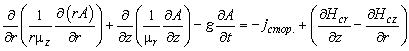 ,
,
где компоненты тензора магнитной проницаемости μx и μy (μz и μr), составляющие коэрцитивной силы Hcx и Hcy (Hcz и Hcr) - постоянные величины в пределах каждого из блоков модели. Сторонняя составляющая тока jстор. предполагается постоянной в пределах каждого блока модели в плоской задаче и обратно пропорциональной радиусу (~1/r) в осесимметричном случае.
Замечание. В нелинейной постановке свойства материалов считаются изотропными (μx = μy или μz = μr) и задаются зависимостью B(H), представленной кубическим сплайном.