Анализ магнитного поля переменных токов состоит в расчете электрического и магнитного поля, возбужденного приложенными переменными (синусоидально изменяющимися во времени) токами или внешним переменным полем.
Изменение поля во времени предполагается синусоидальным. Все компоненты поля и электрические токи изменяются как:
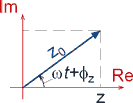
z = z0·cos(ωt + φz),
где z0 - амплитудное (максимальное) значение z, φz - фазовый угол, и ω - угловая частота.
Представление гармонически изменяющейся величины при помощи комплексного числа существенно облегчает анализ. Действительная и мнимая части комплексного числа
z = z0·e i·(ωt + φz),
сдвинуты по фазе на 90 град, по отношению друг к другу, так что их линейная комбинация может представлять произвольный фазовый угол.
|
|
В зависимости от фазового сдвига между двумя осциллирующими компонентами вектора, вектор может вращаться по часовой стрелке или в противоположном направлении, либо колебаться вдоль некоторого направления. В общем случае конец вектора описывает эллипс. Главные полуоси эллипса соответствуют максимальным значениям векторной величины. Отношение длин меньшей и большей полуосей определяет коэффициент поляризации вектора. Последний предполагается положительным при вращении вектора против часовой стрелки и отрицательным в противоположном случае. Нулевой коэффициент соответствует линейной поляризации вектора.
Полный ток в проводнике может рассматриваться как сумма стороннего тока, вызванного приложенным извне напряжением, и вихревого тока, индуцированного переменным магнитным полем
j = jстор. + jвихр
Если расчет поля проводится совместно с присоединенной электрической цепью, уравнение цепи. содержащей массивный проводник в магнитном поле записывается как:
I = U/R - i·ωγs∫A·dS,
где
U - падение напряжения на массивном проводнике, и
R - активное сопротивление проводника на постоянном токе.
Задача формулируется как дифференциальное уравнение в частных производных относительно комплексной амплитуды векторного магнитного потенциала A (B = rot A, B - вектор магнитной индукции). Вектор магнитной индукции предполагается лежащим в плоскости модели (xy или zr), в то время как вектор плотности электрического тока j и векторный магнитный потенциал A ортогональны к нему. Только компоненты jz и Az в плоской постановке и jθ и Aθ в осесимметричном случае отличны от нуля. Будем обозначать их просто j и A. Уравнение для плоской задачи запишется как
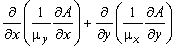- iωgA = -jстор.,
и для осесимметричного случая
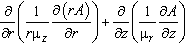- iωgA = -jстор.,
где электропроводность γ и компоненты тензора магнитной проницаемости μx и μy (μz м μr) постоянны в переделах каждого блока модели. Сторонняя составляющая тока jстор. предполагается постоянной в пределах каждого блока модели в плоской задаче и обратно пропорциональной радиусу (1/r) в осесимметричном случае.
Замечание. ELCUT позволяет использовать нелинейные материалы, с магнитной проницаемостью, зависящей от величины поля в задачах магнитного поля переменных токов. Гармоническое приближение использует специально пересчитанную кривую насыщения материала. Пересчет делается так, чтобы эквивалентное значение магнитной проницаемости обеспечивало сохранение средней плотности энергии магнитного поля за период. Редактор кривых намагничивания для задач магнитного поля переменных токов представляет на экране обе кривые: исходную (заданную пользователем) и пересчитанную для частоты задачи.
Описанная формулировка не учитывает член ∂D/∂t в формуле закона Ампера, т.е. пренебрегает плотностью токами смещения. Обычно плотность тока смещения не оказывает заметного влияния до мегагерцовых диапазонов частот.
Замечание. Постоянные магниты не могут быть учтены в задачах данного типа. Здесь предполагается, что все величины, описывающие поле в любой его точке, изменяются во времени синусоидально. Постоянные магниты привносят в систему постоянный во времени магнитный поток.