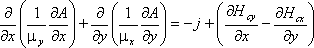 ,
,
Задачи магнитостатики могут быть решены в линейной и нелинейной постановках. Источником поля могут служить сосредоточенные и распределенные токи и токовые слои, постоянные магниты, а также внешние магнитные поля. При решении этих задач используется уравнение Пуассона для векторного магнитного потенциала A (B = rot A, B - вектор магнитной индукции). В рассматриваемых задачах вектор индукции B всегда лежит в плоскости модели (xy или zr), а вектор плотности тока j и векторный потенциал A перпендикулярны к ней. Отличны от нуля только компоненты jz и Az в плоско-параллельном случае или jθ и Aθ в осесимметричных задачах. Мы будем обозначать их просто как j и A. Для плоскопараллельных задач уравнение имеет вид:
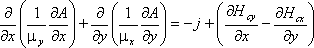 ,
,
а для осесимметричного случая:
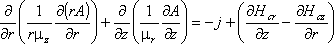 ,
,
где компоненты тензора магнитной проницаемости μx и μy (μz и μr), составляющие коэрцитивной силы Hcx и Hcy (Hcz и Hcr), а также плотность тока j - постоянные величины в пределах каждого из блоков модели.
Замечание. В нелинейной постановке свойства материалов считаются изотропными (μx = μy или μz = μr) и задаются зависимостью B(H), представленной кубическим сплайном.