Главная >> Применение >> Типовые примеры >>

Ёмкость проволочного кольца

емкость заряженного кольца, емкость кольца, заряженное кольцо емкость

Тип задачи
Осесимметричная задача электростатики.

Геометрия

R = 100 мм, a = 8.74 мм.

Дано

Относительная диэлектрическая проницаемость вакуума ε = 1,
Заряд q = 10^-9 Кл

Задание

Найти емкость проволочного кольца и сравнить с аналитическим решением:
C = 4πεε₀ · πR / ln(8R/a), [Ф]. *

Решение
Емкость вычисляется по формуле C = q /U, где U - потенциал, а q - заряд. Поверхность проводника отмечена как "Изолированный проводник" с неизвестным потенциалом. В какой-то момент на поверхности проводника появляется заряд. Затем заряд распределяется по поверхности проводника.
Предполагается, что поле затухает до нуля далеко от кольца. Площадь вычислений ограничена внешней границей, где задан нулевой потенциал.

Результат
Распределение потенциала для случая 10*R.

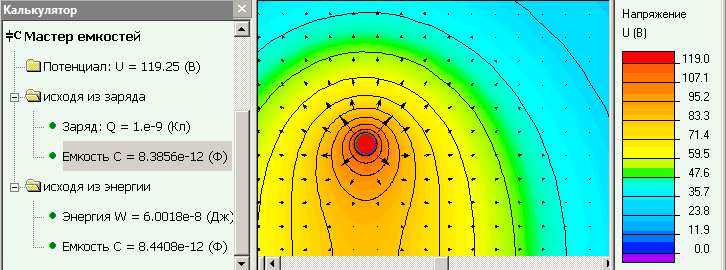
Поскольку потенциал вычисляется при учете нулевого потенциала бесконечности, результат зависит от расстояния до внешней границы. Набор моделей с применением инструмента автоматизации LabelMover.

Расстояние до внешней границы	Напряжение, В	Емкость, пкФ
10*R	119.3	8.38
20*R	123.8	8.08
40*R	125.9	7.94
80*R	127.1	7.87
160*R	127.6	7.84
320*R	127.9	7.82
Теоретическое значение		7.74

• Скачать файлы задачи