Главная >> Применение >> Типовые примеры >>

Механический термодатчик

напряжения, деформации, температура, моделирование термодатчика, температура термодатчика

Два цилиндрических бруска жестко закреплены друг напротив друга, так что между ними образован небольшой зазор. При определенной температуре бруски входят в контакт друг с другом.

Тип задачи
Осесимметричная задача упругих напряжения и деформации.

Геометрия

Дано
Длина латунного бруска L_л = 0.75 дюйма;
модуль Юнга латуни E_л = 15·10⁶ psi (103 ГПа);
коэффициент температурного расширения латуни α_л = 10·10^-6 1/°F (18·10^-6 1/K);
длина магниевого бруска L_м = 1.3 дюйма;
модуль Юнга магния E_м = 6.5·10⁶ psi (44.8 ГПа)
коэффициент температурного расширения магния α_м = 14.5·10^-6 1/°F (26.1·10^-6 1/K);
зазор между брусками δ=0.005 дюймов.

Задание

1. Определить, при какой температуре бруски соприкоснутся друг с другом
2. Определить напряжения, возникающие в бруске из магния при повышении его температуры на ΔT = 300 °F (167 К)

Решение
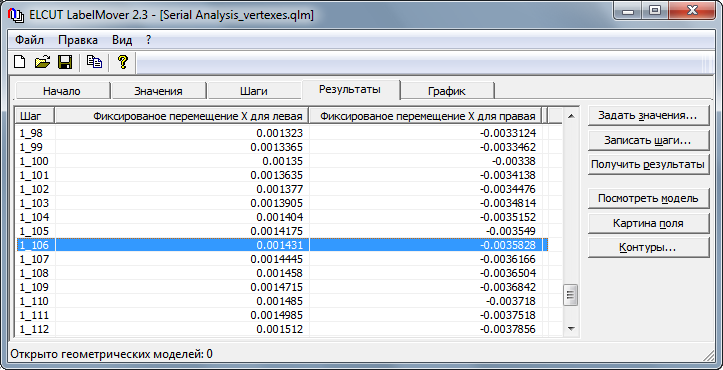
Первая часть является обратной задачей. Она решается путем последовательных расчетов с помощью утилиты LabelMover. Температуры брусков изменяются c шагом 1 К. Для каждого значения температуры определяется удлинение брусков. Таким образом определяется температура Т1, при которой произойдет контакт брусков. До того, как бруски коснутся, механические напряжения в них не возникают.

Задачи определения механических напряжений, возникающих после касания брусков, использует деформированную модель, полученную в первой части (удлиненные бруски). В задаче задано превышение температуры, относительно температуры касания: T2 = ΔT - T1.

Результат
Превышение температуры, при которой бруски коснутся составляет Т1 = 106 K (191 °F).

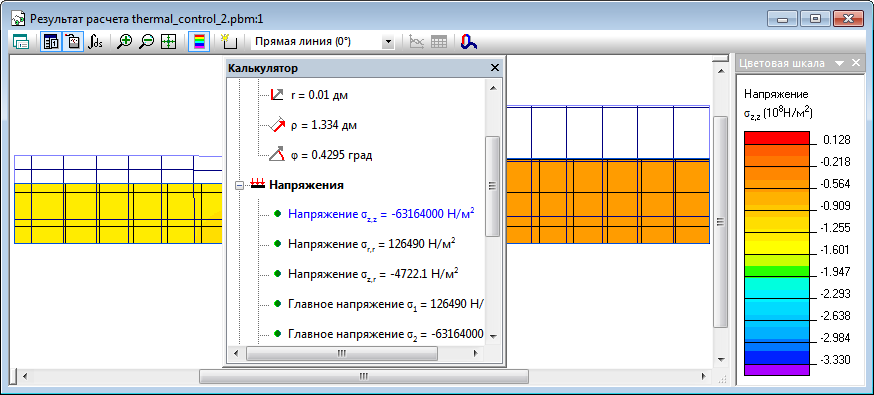
Механические напряжения при перегреве Т2 = 300 - 191 = 109 °F (61 K).

	Температура контакта	Напряжение в магнии
ELCUT	191 °F (106 K)	9170 psi (63.2 МПа)
Теория*	190 °F	9680 psi
Погрешность	0.5%	6%

^*James M. Gere, Stephen P. Timoshenko "Mechanics of materials", Third edition (1990), pp.26-27. ISBN: 0-534-92174-4.

• Видео: Механический термодатчик
  
• Смотреть на YouTube.
• Скачать файлы задачи