Главная >> Применение >> Типовые примеры >>

Быстрое охлаждение бруска

скорость остывания, температура охлаждения, моделирование скорости остывания

Длинный металлический брусок прямоугольного сечения изначально имел температуру T₀. Потом его быстро погрузили в жидкость с температурой T_i. Брусок имеет различные коэффициенты теплопроводности в направлении x и y. Коэффициент конвекции с поверхности бруска равен α.

Тип задачи
Плоско-параллельная задача нестационарной теплопередачи с граничными условиями конвекции.

Геометрия

a = 2 дюйма, b = 1 дюйм

Дано
Брусок обладает разной теплопроводностью по осям λ_x = 34.6147 Вт/K·м, λ_y = 6.2369 Вт/K·м;
Теплоемкость C = 37.688 Дж/кг·K, плотность ρ = 6407.04 кг/м³.
Начальная температура T_i = 37.78°C;
Температура охлаждающей среды T₀ = 260°C, коэффициент конвекции α = 1361.7 Вт/K·м².

Задача
Определить температуры в нескольких контрольных точках сечения бруска после 3 секунд остывания и сравнить с расчетными.

Решение
Модель обладает симметрией и в расчет включена только ¼ от полного сечени. На границах симметрии стоит условие нулевого теплового потока.
Начальная температура пластины задается в свойствах задачи.
Временной шаг был взят равным 0.1 с.

Результаты:
Распределение температуры в сечении бруска после 3 секунд остывания.

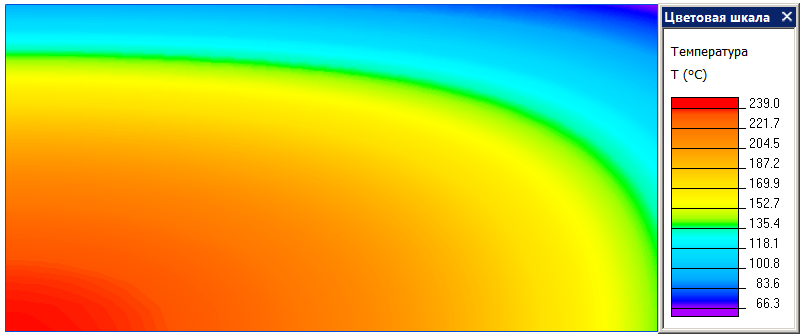
Координаты точки измерения	ELCUT	Источник*
(0,0) дюйм	238.7°C	237.2°C
(2,1) дюйм	66.43°C	66.1°C
(2,0) дюйм	141.2°C	137.2°C
(0,1) дюйм	93.8°C	94.4°C

*Источник:
Schneider P.J., "Conduction heat transfer", Addison-Wesley Publishing Co., Inc, Reading, Mass., 2nd Printing, 1957, страница 261, пример 10-7.

• Скачать файлы задачи