Главная >> Применение >> Типовые примеры >>

Заряженная частица в однородном магнитостатическом поле. Плоско-параллельная задача.

заряженная частица в магнитном поле, траектория заряженной частицы магнитное поле, траектории заряженных частиц

Тип задачи
Плоско-параллельная задача магнитостатики.

Геометрия

Дано
Относительная магнитная проницаемость вакуума μ = 1;
Магнитная индукция внешнего поля B_x = -4 мT.
Заряд (электрона) q = -1.602e-19 Кл
Масса (электрона) m = 9.109e-31 кг
Начальная скорость v_x=v_y=5e6 м/с; v_z = 0 м/с.
Координата вылета частицы: (0; 0; 0) м.

Задание
Рассчитать траекторию движения заряженной частицы в магнитном поле, пренебрегая релятивистскими эффектами.

Решение
Аналитическое решение - спиралевидная траектория.
Радиус в YZ-плоскости R_YZ = v_y / B_x · м/q [м].
Период T = 2π / B_x · m/q [с].
Сила Лоренца F_z = q·v_y·B_x [Н].

Для расчета траектории движения частицы в ELCUT была использована бесплатная утилита Траектории заряженных частиц.

Результаты:

Аналитическое решение:
Радиус в YZ-плоскости R_YZ = (5e6/0.004) · (9.109e-31/1.602e-19) = 0.00711 м.
Период T = (2·3.142/0.04) · (9.109e-31/1.602e-19) = 8.93e-9 с.
Сила Лоренца F_z = 1.602e-19 · 5e6 · 0.04 = 3.20e-15 Н.

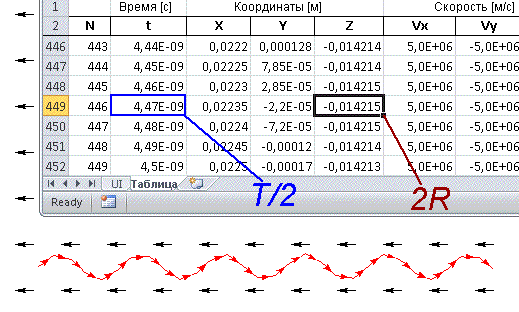
Утилита Траектории заряженных частиц:
Радиус в плоскости YZ R_YZ = 0.14215/2 = 0.00711 м.
Период T = 4.47e-9·2 = 8.94e-9 с.
Сила Лоренца F_z = 3.20e-15 Н.

• Видео: Заряженная частица в однородном магнитостатическом поле. Плоско-параллельная задача.
  
• Смотреть на YouTube.
• Скачать файлы задачи