Главная >> Применение >> Типовые примеры >>

Ёмкость пары параллельных проводов

емкость между параллельными проводниками, емкость параллельных проводников

Тип задачи
Плоско-параллельная задача электростатики.

Геометрия

a1 = 4 мм, a2 = 1 мм, d = 10 мм.

Дано
Относительная диэлектрическая проницаемость воздуха ε = 1,
Заряд q = 1 нКл
Глубина модели L_z = 1 м.

Задача:
Найти взаимную емкость между двумя параллельными проводами и сравнить результат с аналитическим решением*:
C = 2π·ε·ε₀·L_z / ln[ (h1/a1 + √(h1/a1)²-1 ) / (h2/a2 - √(h2/a2)²-1 ) ],
где h1=|d² + a1² - a2²| / 2d и h2=|d² + a2² - a1²| / 2d,

Решение
Глубина модели задается в свойствах задачи.
Чтобы присвоить заряд проводу, ставим на поверхности провода условие "Изолированный проводник" с неизвестным потенциалом. В любой точке на поверхности провода задаем точечный заряд q. Этот заряд автоматически распределяется по поверхности проводника.
ELCUT вычисляет распределение электрического потенциала U. Емкость вычисляется по формуле C = q / (U2-U1).

Результат
Аналитическое решение
h1=|0.01² + 0.004² - 0.001²| / (2·0.01) = 0.00575 м, (h1/a1) = 0.00575/0.004 = 1.4375
h2=|0.01² + 0.001² - 0.004²| / (2·0.01) = 0.00425 м, (h2/a2) = 0.00425/0.001 = 4.25
C= 2·3.142·1·8.854e-12·1 / ln[ (1.4375 + √1.4375²-1 ) / (4.25 - √4.25²-1 ) ] = 18.36 пкФ.

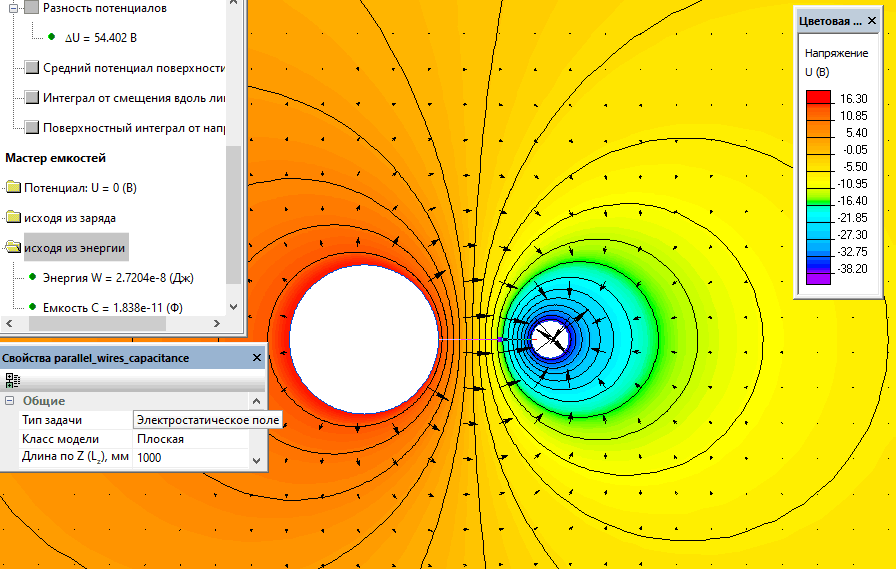
Распределение электрического поля вокруг параллельных проводов, посчитанное в ELCUT.
Разность потенциалов равна U2-U1 = 54.40 В.
Емкость C = 1 нКл / 54.40 В = 18.38 пкФ

*Источник: Демирчян К.С., Нейман Л.Р, Коровкин Н.В, Чечурин В.Л. "Теоретические основы электротехники". В 3-х т. Учебник для вузов. Том 3.

• Видео: Ёмкость пары параллельных проводов
  
• Смотреть на YouTube.
• Скачать файлы задачи