Главная >> Применение >> Типовые примеры >>

Индуктивность длинного соленоида

моделирование катушки соленоида, расчет индуктивности обмотки катушки, моделирование катушки, соленоид, обмотка, расчет индуктивности катушки

Тип задачи
Осесимметричная задача магнитостатики.

Геометрия

R₁ = 30 мм, R₂ = 35 мм.

Дано
Сила тока в проводнике I = 1 A,
число витков N = 100,
длина соленоида l = 0.5 м.

Задача:
Найти индуктивность длинного соленоида, конечными эффектами пренебречь

Решение
Аналитически индуктивность соленоида вычисляется по формуле:
L = μ₀ N ² S / l,
где S - площадь поперечного сечения соленоида (м²).

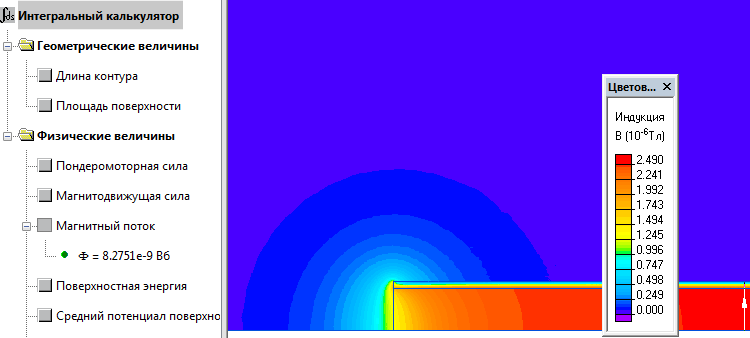
Решение данной задачи в ELCUT сводится к определению магнитного потока через контур, пересекающий соленоид, как показано на рисунке ниже. Непосредственно вычисление величины магнитного потока производится с помощью интегрального калькулятора. Далее, зная поток, можем определить искомую индуктивность соленоида:
L = N ² · Ф / I

Аналитическая формула описывает идеальный соленоид, у которого отсутствуют краевые эффекты и обмотка представлена тонким токовым слоем. С помощью ELCUT можно смоделировать также и реальный соленоид, посчитав поле в окружающем воздухе.

Результаты:
Площадь поперечного сечения соленоида
S = π * ( (R₁ + R₂)/2 )² = 3.142 * ( (0.03+0.035)/2 )² = 0.00332 м².

Индуктивность идеального соленоида
L = 4e-7*3.142 * 100² * 0.00332 / 0.5 = 83.45 мкГн.

Магнитное поле идеального соленоида:

Магнитное поле реального соленоида:

	Индуктивность L
Идеальный соленоид, теория	83.45 мкГн
Идеальный соленоид, ELCUT	83.55 мкГн
Реальный соленоид, ELCUT	82.75 мкГн

• Скачать файлы задачи