Главная >> Применение >> Типовые примеры >>

Равновесная температура

электрическая машина нагрев статора, температура паза статора, паз статора температура

Горячий стальной шар погружен в ёмкость с холодной водой. Определить установившуюся температуру в системе.

Тип задачи

Осесимметричная задача теплопроводности.

Геометрия

Объем шарика V_сталь = 65.4·см³, объем воды V_вода = 3600 cm³.

Дано
T_сталь= 85°C, T_вода=20°C;
Плотность стали ρ_сталь = 7800 кг/м³,
Плотность воды ρ_вода = 1000 кг/м³,
Теплоёмкость стали C_сталь = 460 Дж/кг·K,
Теплоёмкость воды C_вода = 4200 Дж/кг·K.

Задача:
Рассчитать установившуюся равновесную температуру.

Решение
Мы должны разделить два тела, чтобы предотвратить теплообмен между ними на начальном этапе. В нестационарной задаче тела связаны периодическим граничным условием T1=T2.

Согласно первому закону термодинамики энергия изолированной системы сохраняется^*:
(CρV)_вода·(T_вода - T) + (CρV)_сталь·(T_сталь - T) = 0, где
T - температура установившегося равновесия.

Результат
Аналитическое решение
Энергия запасенная в воде (CρV)_вода = 4200·1000·3600·10^-6 = 15120 [Дж/K]
Энергия запасенная в стали (CρV)_сталь = 460·7800·65.4·10^-6 = 235 [Дж/K]

Уравнение сохранения энергии
15120·(20 - T) + 235·(85 - T) = 0
Установившаяся температура в системе T = 20.99°C

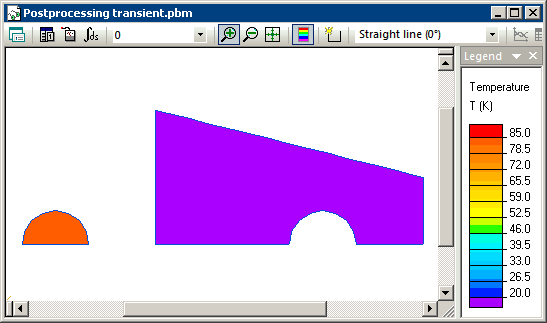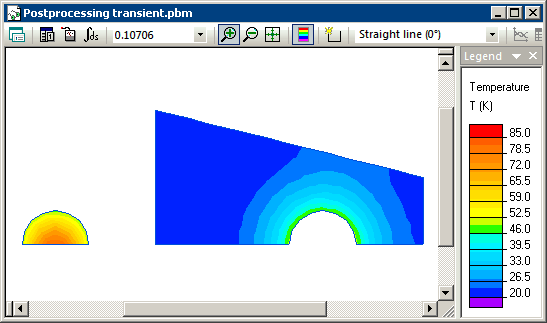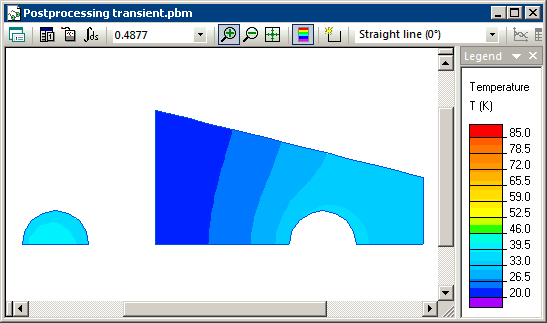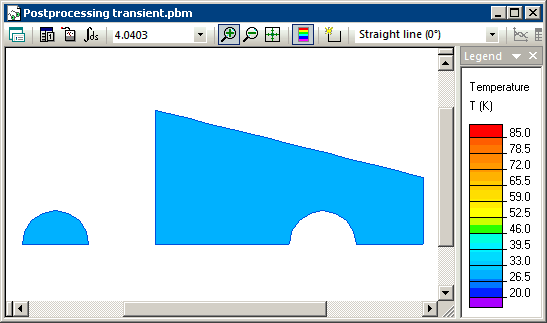
Распределение температуры, посчитанное в ELCUT для разных моментов времени:

^*A textbook of Engineering Thermodynamics, R.K.Rajput, Luxmi publication (P) Ltd, Fourth edition, 2010.

• Скачать файлы задачи