продукт
Главная >> Применение >> Типовые примеры >>
Закон Фарадея для электромагнитной индукции
электромагнитная индукция, постоянный магнит, динамика магнитного поля
Пример показывает появление тока в замкнутой катушке, при вдвижении в катушку постоянного магнита.
Тип задачи
Осесимметричная задача нестационарного магнитного поля.
Геометрия
Дано
Катушка намотана проводом 0.25 мм² и содержит 200 витков
Коэрцитивная сила постоянного магнита Hc = 500 кА/м.
Скорость движения магнита v = 9 см/с.
Задача:
Построить график изменение тока от времени в катушке
Решение
Для моделирования движения магнита коэрцитивная сила представлена формулой от координат (x) и времени (t).
Hc*impulse(x + v*(t-1.02)*step(t-1.02),0.08,0.10)
функция impulse описывает пространственный импульс вдоль оси х в пределах от 0.08 м до 0.10 м (длина импульса 20 мм и равна длине магнита).
Импульс перемещается в пространстве со скоростью v.
Так как нестационарная задача решается с нулевым начальным приближением, то требуется время, чтобы возмущения вызванные появлением магнита успокоились. Поэтому введена задержка начала движения на 1.02 с. Задержка реализована функцией step.
Подробно посмотреть характер поведения графика можно используя онлайн утилиту Визуализации формул из ELCUT
Результаты
График зависимости тока и распределение индукции в один из моментов времени.
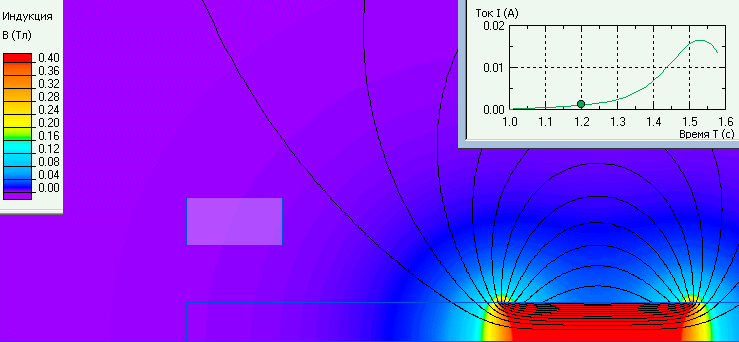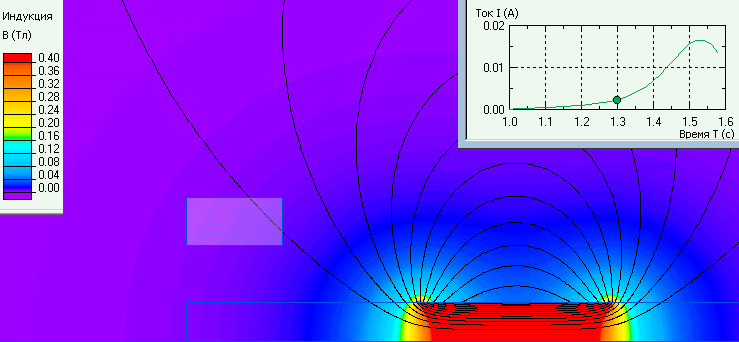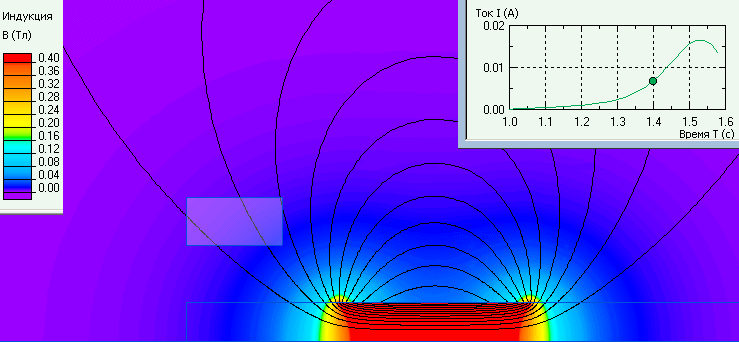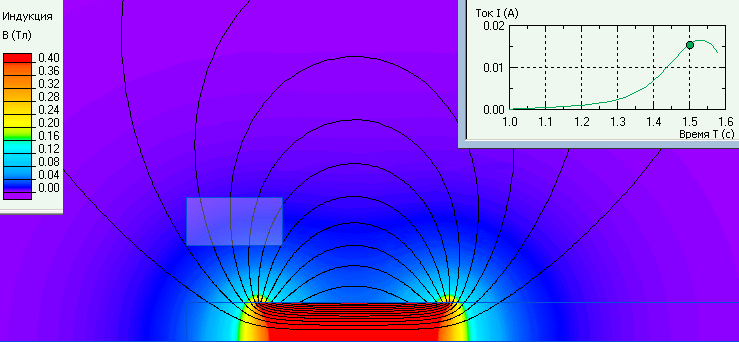
Ссылка: Википедия: Закон электромагнитной индукции Фарадея
