Главная >> Применение >> Типовые примеры >>

Тепловые потери стенки кастрюли

кухонная кастрюля тепловая модель

Тип задачи
3D задача стационарной теплопередачи с граничными условиями конвекции.

Геометрия

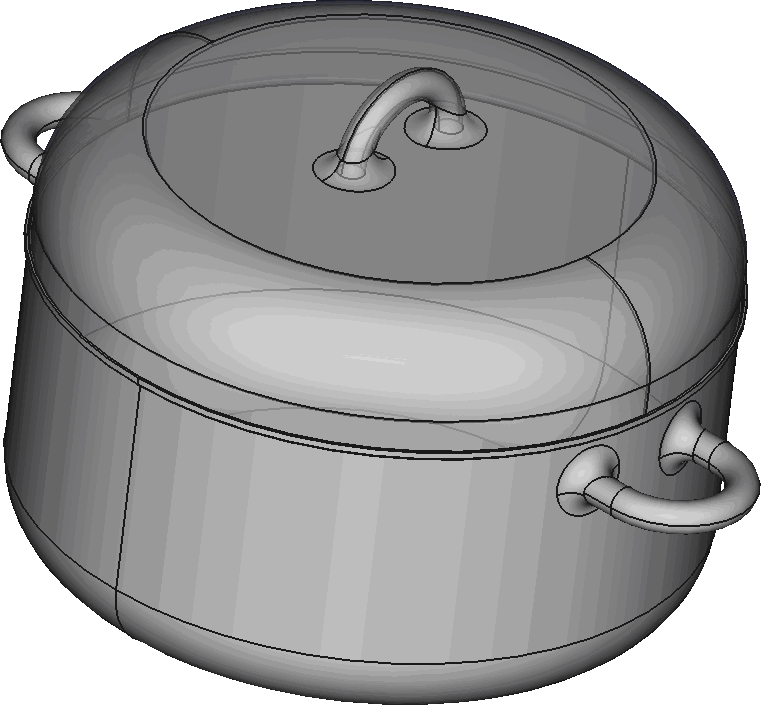
Дано
Теплопроводность металла λ = 40 Вт/K·м.
Температура воздуха T₀ = 20 °C, коэффициент конвекции α = 15 Вт/K·м².
Температура внутри кастрюли T_воды = 100 °C.

Задача:
Кастрюля нагревается до температуры кипения воды. Определить требуемую мощность нагревателя для поддержания кипения.

Решение
Тогда, требуемая мощность нагревателя равна мощности тепловых потерь. В задаче не сказано, как нагревается кастрюля. Предполагаем, что нагрев происходит со стороны дна, а теплопотери происходят с боковых поверхностей и со стороны крышки. Тогда на охлаждаемых поверхностях следует задать граничное условие конвекции, а на дне не задаем ничего (нулевой поток). На внутренней поверхности кастрюли задана температура 100 °C.
Геометрия обладает симметрией, и для ускорения счета можно смоделировать только 1/2 от кастрюли. При этом, полученный результат потерь следует умножить на 2, для получения полной мощности потерь.

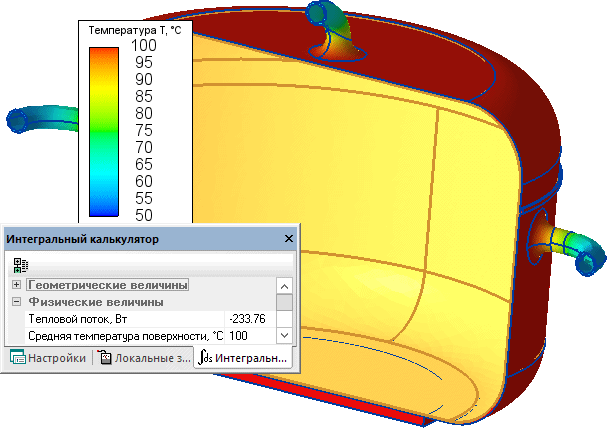
Результаты:
Распределение температуры по стенкам кастрюли. Суммарная мощность потерь (требуемая мощность нагревателя) составляет 2*233=566 Вт.

• Скачать файлы задачи