Главная >> Применение >> Типовые примеры >>

Естественная конвекция с поверхности вертикальной пластины

температура, коэффициент конвекции расчет, коэффициент конвекции вертикальная поверхность, вертикальная поверхность естественная конвекция

Вертикальная стальная пластина разделяет две воздушных среды с разными температурами

Тип задачи
Плоско-параллельная задача стационарной теплопередачи.

Геометрия

Высота пластины l = 1000 мм, толщина пластины d = 2 мм, площадь поверхности пластины 1 м².

Дано
температура воздуха слева от пластины T₁ = 20°C,
температура воздуха справа от пластины T₂ = -10°C,
теплопроводность пластины λ_пласт = 0.4 Вт/(м·K),
теплопроводность наружного воздуха λ_возд = 0.027 Вт/(м·K).

Задание
Определить температуры левой и правой поверхностей пластины и тепловой поток через них.

Решение
Тепловой поток идет от более тёплой области к более холодной (в нашей модели слева направо через стенку). Тепловой поток внутри стенки передаётся за счёт теплопроводности. Тепло передается от стенки к воздуху за счёт конвекции. Коэффициенты конвекции зависят от многих параметров, включая температуру среды, форму и ориентацию поверхностей.
Вычисление коэффициентов конвекции выполнено в калькуляторе коэффициента конвекции для естественных условий. Температуры поверхностей пластины для расчета коэффициентов конвекции будем оценивать равными средней температуре пластины, которую можно принять за T_пл = (T₁+T₂)/2 = 5 °C

Средние коэффициенты конвекции с поверхностей пластины
с теплой стороны α₁ = 3.6 Вт/(м²·K); с холодной стороны α₂ = 3.7 Вт/(м²·K).

Результат
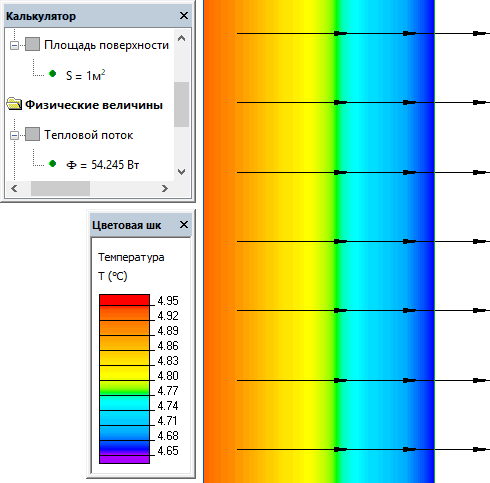
Поток тепла: Ф = 54 Вт / м².
Температура левой поверхности пластины: T₁ = 4.9 °C.

Температура правой поверхности пластины: T₂ = 4.6 °C.

Полученные значения температур близки к начальному предположению о температуре поверхностей. Поэтому проведение итерационного процесса уточнения коэффициентов конвекции не требуется.

• Скачать файлы задачи