Главная >> Применение >> Типовые примеры >>

Естественная конвекция с поверхности горизонтальной трубы

конвекция, температура, теплопроводность, тепловой поток, моделирование трубы

Горизонтальная стальная труба, полностью заполненная текущей по ней горячей водой, окружена неподвижным воздухом.

Тип задачи
Плоско-параллельная задача стационарной теплопередачи.

Геометрия

Дано
внутренний диаметр трубы D1 = 120 мм,
наружный диаметр трубы D2 = 140 мм,
температура воды T_вода = 90°C,
температура окружающего воздуха T_возд = 20°C,
теплопроводность трубы λ_труб = 0.4 Вт/(м·K).

Задание
Определить внешнюю температуру трубы и тепловой поток на метр длины.

Решение
Текущая по трубе горячая вода нагревает её внутреннюю поверхность до своей температуры. Тепло с поверхности трубы уходит в окружающую среду в результате конвекции. Коэффициент конвекции зависит от многих параметров, включая температуру среды, форму и ориентацию поверхности.
Вычисление коэффициентов конвекции выполнено в калькуляторе коэффициента конвекции для естественных условий. Температуры поверхности трубы для расчета коэффициента конвекции примем T_s = T_вода = 90 °C.
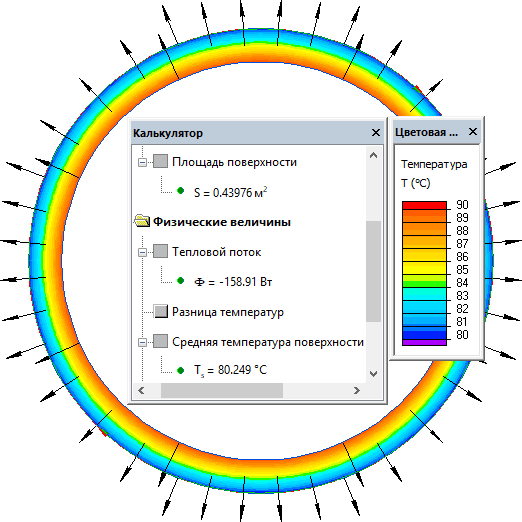
Средний коэффициент конвекции с поверхности трубы: α = 6 Вт/(м²·K).

Результат
Поток тепла на метр длины трубы: Ф = 159 Вт. Температура поверхности трубы: T_s = 80 °C.

Полученное значение температуры близко к начальному предположению о температуре поверхности. Поэтому проведение итерационного процесса уточнения коэффициента конвекции не требуется.

• Скачать файлы задачи