Главная >> Применение >> Типовые примеры >>

Естественная конвекция с поверхности сферы

конвекция, температура, теплопроводность, тепловой поток, расчет коэффициентов конвекции, расчет теплопроводности, расчет теплового потока

Теплопередача через стенку сферической формы в окружающее пространство.

Тип задачи
Плоско-параллельная задача стационарной теплопередачи.

Геометрия

Радиус сферы R = 75 мм, толщина стенки сферы d = 3 мм.

Дано
температура внутренней поверхности сферы T₀ = 20 °C,
температура воздуха T = -10 °C,
теплопроводность сферы λ_сфера = 0.4 Вт/(м·K).

Задание
Определить температуру наружной поверхности сферы и тепловой поток через неё.

Решение
Тепловой поток идет от более тёплой области к более холодной (в нашей модели изнутри наружу, через стенку сферы). Тепловой поток внутри стенки передаётся за счёт теплопроводности. Тепло передается от стенки сферы к воздуху за счёт конвекции. Коэффициент конвекции зависит от многих параметров, включая температуру среды и геометрию поверхности.
Вычисление коэффициента конвекции выполнено в калькуляторе коэффициента конвекции для естественных условий. Температуру наружной поверхности стенки сферы для расчета коэффициента конвекции примем равной T_s = T₀ = +20 °C.
Средний коэффициент конвекции с поверхности сферы: α = 4.8 Вт/(м²·K).

Результат
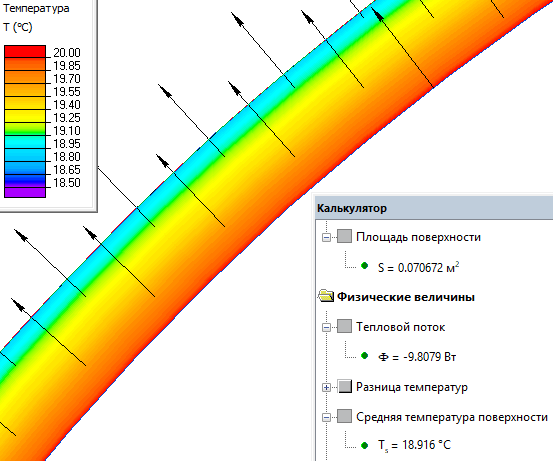
Поток тепла: Ф = 10 Вт (площадь поверхности сферы 0.071 м²).
Температура внешней поверхности сферы: T_s = 19 °C.
Полученное значение температуры близко к начальному предположению о температуре поверхности. Поэтому проведение итерационного процесса уточнения коэффициента конвекции не требуется.

• Скачать файлы задачи