Главная >> Применение >> Типовые примеры >>

Квадрупольный заряд

квадруполь, электрическое поле, электрическое поле квадруполь

Заряды расположены в вершинах квадрата 1x1 [м].

Тип задачи электростатика.

Геометрия 3D вытягивание.

Дано
Относительная диэлектрическая проницаемость воздуха ε_r = 1,
Заряд электрона q = 1.602e-19 Кл.
Заряды квадруполя Q1 = 1*q, Q2 = 2*q, Q3 = 3*q, Q4 = -6*q.

Задание
Рассчитать распределение напряженности электрического поля вдоль оси z.

Решение
Аналитическая формула выводится из закона Кулона^*:
E(z) = k * q/r² [В/м], где
k=8.988e9 константа,
r - расстояние от заряда q.

Для произвольной точки на оси z можно найти компоненты напряженности электрического поля от каждого заряда:
E1z(z)= k * Q1 / r² * sin(β),
E1x(z)= k * Q1 / r² * cos(β) * -cos(α1),
E1y(z)= k * Q1 / r² * cos(β) * -sin(α1),
E1z(z)= ..........
..................
где α1 = <XOQ1 (угол в плоскости XY между векторами O-X и O-Q1).
(в нашей модели α1 = 3π/4, α2 = π/4, α3 = -π/4, α4 = -3π/4).

Компоненты напряженности электрического поля равны:
Ex(z) = k / r² * cos(β) * (-Q1*cos(α1) - Q2*cos(α2) - Q3*cos(α3) - Q4*cos(α4)),
Ey(z) = k / r² * cos(β) * (-Q1*sin(α1) - Q2*sin(α2) - Q3*sin(α3) - Q4*sin(α4)),
Ez(z) = 0.

Результаты:
Аналитическое решение для z=0: cos(β) = 1, r=0.707 m;
Ex(0) = 8.988e9 / (0.707)² * 1 * ( -q*cos(3π/4) - 2q*cos(π/4) - 3q*cos(-π/4) + 6q*cos(-3π/4)) = 1.271e10*(-10q) = 2.04e-8 В/м;
Ey(0) = 8.988e9 / (0.707)² * 1 * ( -q*sin(3π/4) - 2q*sin(π/4) - 3q*sin(-π/4) + 6q*sin(-3π/4)) = 1.271e10*(-6q) = 1.22e-8 В/м;
Ez(0) = 0 В/м.

Напряженность электрического поля, рассчитанная в ELCUT:

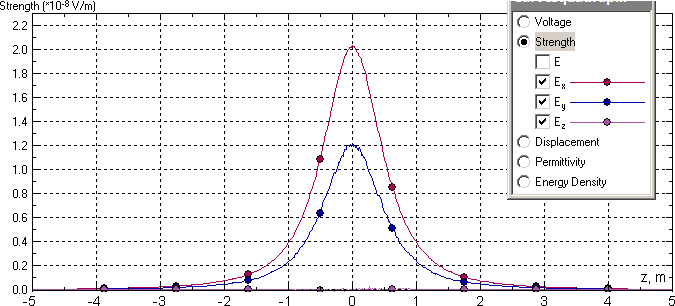
*Ссылка: Закон Кулона на Википедии.

• Скачать файлы задачи