продукт
Главная >> Применение >> Типовые примеры >>
моделирование заряженной частицы в электрическом поле, траектория электрона
Тип задачи
Осесимметричная задача электростатики.
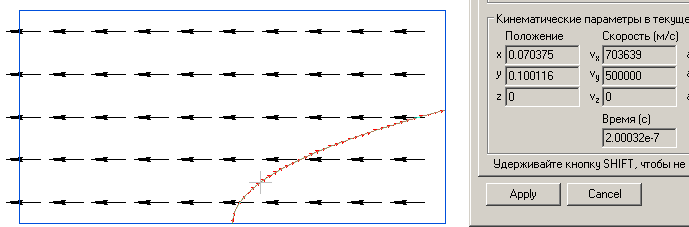
Геометрия
Дано
Относительная диэлектрическая проницаемость вакуума ε = 1;
Положительный потенциал U+ = 20 В.
Заряд (электрона) q = -1.602e-19 Кл
Масса (электрона) m = 9.109e-31 кг
Начальная скорость vr = 500 000 м/с; vz = vφ = 0 м/с.
Координата вылета частицы: (0; 0; 0).
Задача:
Рассчитать траекторию движения заряженной частицы, пренебрегая релятивистскими эффектами.
Решение
Аналитическое решение - параболическая траектория
x(t) = 0 [м],
y(t) = vy · t [м],
z(t) = 0.5 · Fz / m · t² [м],
где Fz - z-компонента силы Лоренца,
t - время.
Траектория движения частицы может быть рассчитана с помощью встроенной функции ELCUT или с помощью бесплатной утилиты Траектории заряженных частиц.
Результаты:
Напряженность электрического поля Ez = -20 В/м, Er = 0 В/м
Сила Лоренца: Fφ = q · Ez = -1.602e-19 · (-20) = 3.204e-18 Н,
x(t) = 0 м,
y(t) = 5e5·t м,
z(t) = 0.5·3.204e-18/9.109e-31 ·t² м.
Координаты частицы (x; y; z) м | |||
| Время | Теория | ELCUT | Утилита Траектории заряженных частиц |
| 0 с | (0; 0; 0) | (0; 0; 0) | (0; 0; 0) |
| 1e-7 с | (0; 0.050; 0.018) | (0; 0.050; 0.018) | (0; 0.050; 0.018) |
| 2e-7 с | (0; 0.100; 0.070) | (0; 0.100; 0.070) | (0; 0.100; 0.070) |
| 3e-7 с | (0; 0.150; 0.158) | (0; 0.150; 0.158) | (0; 0.150; 0.158) |
| 4e-7 с | (0; 0.200; 0.281) | (0; 0.200; 0.281) | (0; 0.200; 0.281) |
| 5e-7 с | (0; 0.250; 0.440) | (0; 0.250; 0.440) | (0; 0.250; 0.440) |