Главная >> Применение >> Типовые примеры >>

Естественная конвекция с поверхности наклонённой пластины

конвекция, температура, теплопроводность, тепловой поток, расчет коэффициентов конвекции, температура пластины, теплопроводность пластины, тепловой поток пластины

Наклоненная под углом к вертикали стальная пластина отдает тепло в окружающее пространство.

Тип задачи
Плоско-параллельная задача стационарной теплопередачи.

Геометрия

Длина пластины l = 1000 мм, толщина пластины d = 2 мм, угол наклона θ=50°.
Площадь пластины 1 м².

Дано
температура нижней части пластины T₀ = 20 °C,
температура воздуха выше пластины T = -10 °C,
теплопроводность пластины λ_пласт = 0.4 Вт/(м·K)

Задание
Определить температуру верхней поверхностей пластины и тепловой поток через неё.

Решение
Нижняя часть пластины нагрета до 20°C, а температура воздуха над верхней частью -10°C, поэтому тепловой поток теплопроводности внутри пластины направлен к внешней поверхности. Верхняя поверхность пластины теплее окружающего её воздуха, поэтому тепловой поток направлен от поверхности в окружающее холодное пространство за счет конвекции. Коэффициент конвекции зависит от многих параметров, включая температуру среды, форму и ориентацию поверхностей.
Вычисление коэффициентов конвекции выполнено в калькуляторе коэффициента конвекции для естественных условий. Температуру наружной поверхности стенки для расчета коэффициента конвекции примем равной T_пов = T₀ = +20 °C.
Средний коэффициент конвекции с поверхности пластины: α = 4 Вт/(м²·K).

Результат
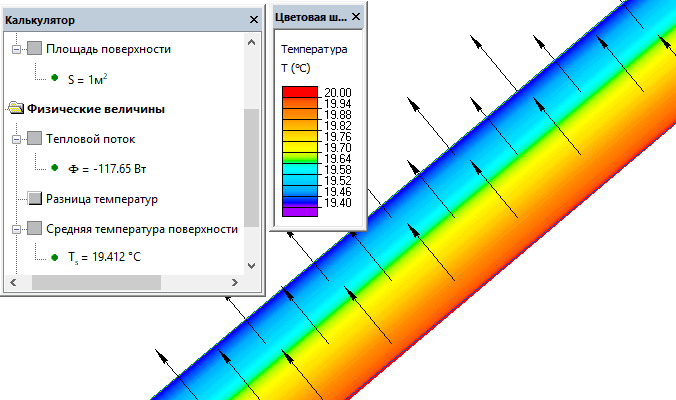
Поток тепла: Ф = 117 Вт (площадь пластины 1 м²).
Температура верхней поверхности пластины: T_пов = 19.4 °C.
Полученное значение температуры близко к начальному предположению о температуре поверхности. Поэтому проведение итерационного процесса уточнения коэффициента конвекции не требуется.

• Скачать файлы задачи