Главная >> Применение >> Типовые примеры >>

Двухпроводная экранированная линия передачи

линия передачи импеданс, омические потери в экране, распределение тока в линии электропередач, импеданс линии электропередач, потери линии электропередач

Тип задачи
Плоско-параллельная задача магнитного поля переменных токов.

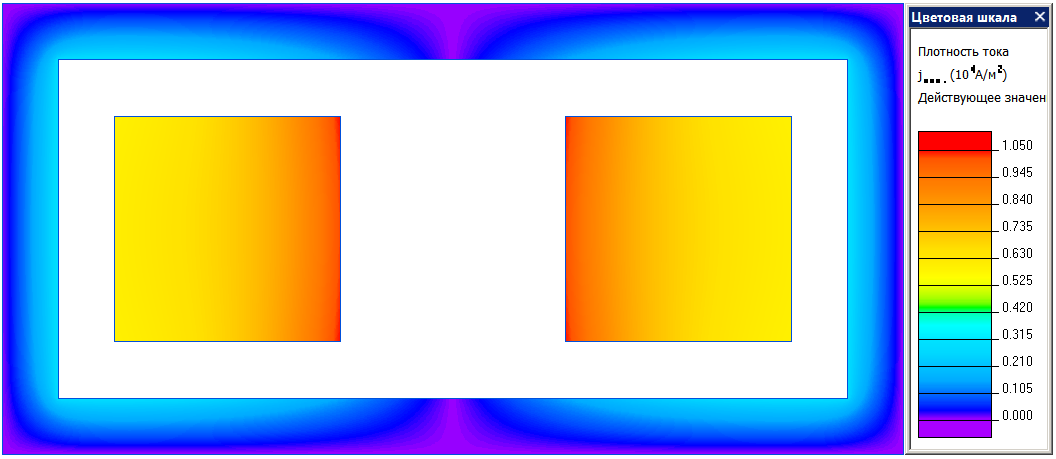
Геометрия

Два проводника квадратного сечения с одинаковыми токами, противоположными по фазе помещены внутри прямоугольного ферромагнитного экрана. Все размеры указаны в миллиметрах.

Дано
Электропроводность меди σ = 56 МСм/м;
Магнитная проницаемость экрана μ = 100;
Электропроводность экрана σ = 1·10⁶ См/м;
Ток в проводниках I = 1 A;
Частота f = 100 Гц.

Задание
Найти распределение токов внутри проводников, импеданс линии и омические потери в экране.

Решение
Предполагая, что магнитный поток целиком содержится в экране, мы можем задать граничное условие Дирихле на его внешней поверхности.
Комплексное сопротивление (импеданс) линии на единицу длины может быть вычислен по формуле Z = ( V₁ - V₂ ) / I,
где V₁ и V₂ - падения напряжения на единицу длины в каждом из проводников. Вследствие симметрии эти напряжения равны по величине и противоположны по знаку. Чтобы узнать падение напряжения, включите режим Локальные Значения (меню Вид) окна анализа результатов и щелкните мышью в любую точку проводника.

Импеданс линии Z = 0.000484 + i 0.000736 Oм/м.
Омические потери в экране составляют P = 0.0000427 Вт/м.

Плотность тока в симметричной двухпроводной линии:

• Скачать файлы задачи