Главная >> Применение >> Типовые примеры >>

Проводник в ферромагнитном пазу

моделирование паза электрической машины, распределение тока в пазу, расчет импеданса проводника в пазу, распределение тока в пазу встроенного проводника, расчет импеданса проводника

Тип задачи
Плоско-параллельная задача магнитного поля переменных токов.

Геометрия

По массивному медному проводнику, уложенному в паз электрической машины, течёт переменный ток I частоты f.

Дано
Магнитная проницаемость воздуха μ = 1;
Магнитная проницаемость меди μ = 1;
Электропроводность меди σ = 58,005,000 См/м;
Ток в проводнике I = 1 A;
Частота f = 45 Гц.

Задание
Найти распределение токов внутри проводника и его импеданс.

Решение
Предполагая бесконечную магнитную проницаемость стенок паза, заменим их граничным условием Неймана. Мы также предполагаем, что магнитный поток не выплескивается в воздушный зазор через верхнюю границу проводника, так что ее можно описать нулевым граничным условием Дирихле.

Комплексное сопротивление (импеданс) проводника на единицу длины может быть получен из уравнения: Z = U / I,
где U падение напряжения на единицу длины. Это падение напряжения может быть получено в окне анализа результатов расчета при помощи команды Локальные значения в меню Вид. В этом режиме следует щелкнуть мышью любую точку в пределах проводника.

Сравнение результатов
Плотность тока в проводнике в пазу:

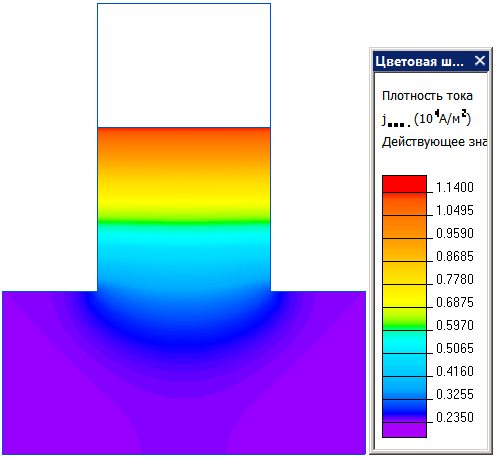
	Re Z (Ом/м)	Im Z (Ом/м)
Источник	0.00017555	0.00047113
ELCUT	0.00017550	0.00047111

Источник
A. Konrad, "Integrodifferential Finite Element Formulation of Two-Dimensional Steady-State Skin Effect Problems", IEEE Trans. Magnetics, Vol MAG-18, No. 1, January 1982.

• Скачать файлы задачи