Главная >> Применение >> Типовые примеры >>

Многослойный высоковольтный проходной изолятор

емкостной изолятор, многослойный изолятор емкость, расчет высоковольтного изолятора, напряженность, напряжение, изолированный проводник, емкость

Пример подготовил доктор Влодзимеж Калат (Wlodzimierz Kalat)

Многослойный высоковольтный проходной изолятор состоит из нескольких слоев изоляции отделенных очень тонкими "плавающими" слоями проводников. Их постоянный, но неизвестный потенциал определяется после расчета распределения электростатического поля и может контролироваться за счет изменения длины, толщины и диэлектрической проницаемости слоев изоляции. С технологической точки зрения только определенные размеры могут обеспечить равномерное распределение радиальной составляющей напряженности электрического поля. Тем самым обеспечивается наилучшее использование изоляция и поле вблизи изолятора выравнивается наилучшим образом.

Теоретически, для обеспечения равномерного распределения электрического поля (E(r)=const) вместо логарифмического, необходимо бесконечное число свободных электродов. В действительности, допустимо только конечное число слоев, обычно 10-12.

Главной целью примера является моделирование очень простого (их 2-слоев) высоковольтного изолятора, расчёт распределения радиальной компоненты напряженности электрического поля и сравнение получившихся результатов с теоретическими. Условие равенства E_r,max в каждом слое (E_1r,max = E_2r,max) дает возможность найти длину изолированного электрода и его потенциал.

Тип задачи:
Осесимметричная задача электростатики.

Геометрия:

______________________________________нулевой потенциал
 | |
 воздух | |<-- барьер (заземленный электрод)
 | |
 |_|
 / \ <-- 2-й слой изоляции
 /__2__\ <-- изолированный электрод
 / \ <-- 1-й слой изоляции
_______________/____1____\______________ высокий потенциал
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ось симметрии

Все размеры заданы в сантиметрах. Длина (L) изолированного электрода должна быть посчитана перед построением модели.
Радиус заземленного электрода r₃ = 30 см
Радиус отверстия в барьере r₂ = 6 см
Радиус изолированного электрода r₁ = 4 см
Радиус высоковольтного электрода r₀ = 2 см

Дано
Относительная диэлектрическая проницаемость изоляции (эпоксидная резина) ε = 5.0;
Напряжение между электродами U = 110 кВ.

Решение

Чтобы было проще проверить результат с помощью теоретической формулы, наклон края изолятора сделан перпендикулярным оси симметрии.

Результаты:

1. Три емкости: C₁, C₂ - слоев и C₁₀ - между электродом с неизвестным потенциалом и землей рассчитаны с помощью интегральных параметров (запасенной энергии и поверхностного заряда). Условие баланса зарядов Q₁ = Q₂ + Q₁₀ приводит к уравнению для определения длины (L) электрода с неизвестным потенциалом.

   ____________________________________нулевой потенциал
    | | |
    | | |
    |_____| |
    | | | === C10
    C2-->| === | |
    __|__|__|__|
    | | |
    | === C1 |
   __________|_____|_____|_____________высокий потенциал
    
    _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ ось симметрии
   

2. Максимальное значение E(r) вдоль среднего сечения изолятора найдено по графику. Можно заметить равенство E_1r,max и E_2r,max.
3. Неизвестный потенциал электрода U определяется как "Средний потенциал поверхности" или с помощью вычисления локальных значений.
   

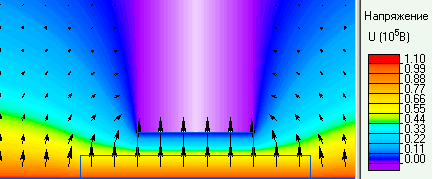
   	C10[пФ]	C1[пФ]	C2[пФ]	Er1[кВ/см]	Er2[кВ/см]	U[кВ]
   Теория	3.84	84.64	68.51	36.57	36.57	59.31
   Способ 1	3.97	81.37	70.10	30.97	31.16	57.51
   Способ 2	3.52	79.68	75.90	-	-	-

   Замечания:
   1. Значения емкости в ELCUT были определены двумя способами: через электрическую энергию (2·W / U²); через полный заряд электрода (Q/U).
   2. Расхождения между теорией и полученный результатом обусловлены в первую очередь ограничением на число узлов в студенческой версии ELCUT.

• Скачать файлы задачи