продукт
Главная >> Применение >> Типовые примеры >>
Гармонический анализ пилообразной функции
анализ Фурье треугольная пила, гармонический анализ пилообразной функции
Этот пример специально подготовлен для проверки точности надстройки "Гармонический анализатор" (входит в состав ELCUT).
В прямоугольном волноводе, состоящим из двух электродов, задано пилообразное распределение потенциала. Определить гармонический состав сигнала.
Тип задачи
Плоско-параллельная задача электростатики
Геометрия
Дано
Относительная диэлектрическая проницаемость воздуха ε = 1,
Потенциалы на границах - пилообразная функция.
Задание
Разложить на гармоники кривую распределения потенциала. Определить амплитуды гармоник, полученных с помощью гармонического анализатора и сравнить с аналитическими значениями.
Решение
Потенциал на ребрах задан в виде составной функции:
U(0≤x<1.507) = 2·x
U(x=1.507) = 0
U(1.507<x≤3.142) = 2·x - 2·π
Аналитический анализ "пилы" дает бесконечный ряд гармоник.*
f(x) = 2 · ( sin(x) - sin(2x) / 2 + sin(3x) / 3 - ... + (-1)n+1·sin(nx) / n )
Результат
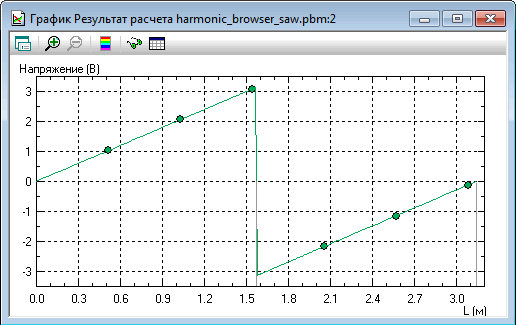
Распределение потенциала по нижнему ребру
Окно гармонического анализатора
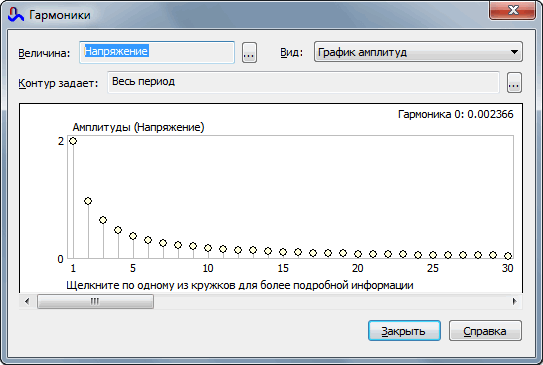
Гармонический анализатор позволяет вычислить первые сто гармоник.
| Гармоника | Амплитуда | Погрешность | |
|---|---|---|---|
| ELCUT | Теория | ||
| 1 | 2 | 2 | - |
| 2 | 0.9999 | 1 | - |
| 3 | 0.6666 | 0.6666 | - |
| 4 | 0.4999 | 0.5 | - |
| 5 | 0.3999 | 0.4 | - |
| 10 | 0.1999 | 0.2 | 0.05% |
| 20 | 0.0998 | 0.1 | 0.2% |
| 50 | 0.0383 | 0.04 | 5% |
| 100 | 0.0168 | 0.02 | 15% |
*Mathematical Methods for Physicists. A Comprehensive Guide. 7th Edition. George Arfken, Hans Weber, Frank Harris, p 937-938. ISBN 978-0-12-384654-9.
