Главная >> Применение >> Типовые примеры >>

Двухпроводная линия передачи

печатная плата электрическая емкость, расчет емкости, моделирование линия электропередачи

Тип задачи
Плоско-параллельная задача электростатики.

Геометрия

Область задачи ограничена заземленным слоем внизу и бесконечна в трех других направлениях.

Дано
Относительная диэлектрическая проницаемость среда:
- воздух, ε = 1;
- диэлектрик, ε = 2.

Задание
Определить собственную и взаимную емкость проводников.

Решение
Для решения теоретически бесконечной задачи определим область расчета как прямоугольник, достаточно большой, для того чтобы исключить влияние краевых эффектов. Для вычисления матрицы емкостей установим потенциалы U = 1 В у одного проводника и U = 0 у другого.

Собственная емкость:  C₁₁ = C₂₂ = Q₁ / U₁

Взаимная емкость:  C₁₂ = C₂₁ = Q₂ / U₁ ,

Заряды проводников Q₁ и Q₂ вычисляются как интегралы вдоль прямоугольных контуров, проведенных вокруг проводников 1 и 2 с отступом от их границ. Мы выбрали в качестве контуров для вычисления зарядов Q₁₁ и Q₁₂ прямоугольники -6 ≤ x ≤ 0, 0 ≤ y ≤ 4 и 0 ≤ x ≤ 6, 0 ≤ y ≤ 4 соответственно.

Результаты
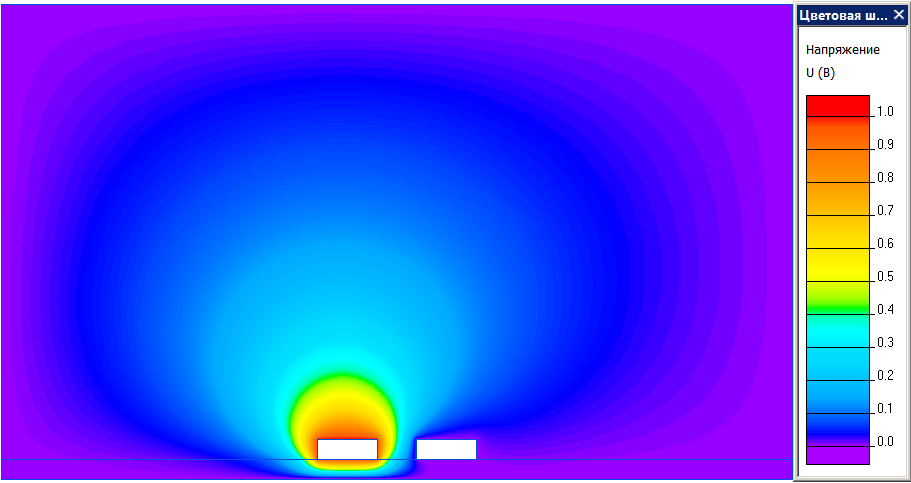
Распределение потенциала в двухпроводной линии:

	C11 (Ф/m)	C12 (Ф/m)
Источник	9.23·10 -11	-8.50·10 -12
ELCUT	9.43·10 -11	-8.57·10 -12

Источник:
A. Khebir, A. B. Kouki, and R. Mittra, "An Absorbing Boundary Condition for Quasi-TEM Analysis of Microwave Transmission Lines via the Finite Element Method", Journal of Electromagnetic Waves and Applications, 1990.

• Скачать файлы задачи