продукт
Главная >> Применение >> Типовые примеры >>
расчет Джоулевых потерь силового кабеля, калькулятор импеданса кабеля, импеданс кабеля, кабельный калькулятор, расчет сопротивления кабеля, САПР кабеля
Высоковольтный четырехпроводный кабель состоит из трех фазных проводников и одного нулевого. Фазный проводник в сечении имеет форму треугольника со скругленными углами, а нулевой проводник – круглое сечение. Все проводники алюминиевые, изолированные. Кабель в целом имеет трехслойную изоляцию – внутренняя электрическая изоляция, затем защитный слой стальной ленты и внешняя защитная изоляция. Свободное пространство между изолированными проводниками заполнено диэлектриком, в роли которого может быть и воздух.
На практике часто требуется спроектировать кабель по заданному сечению фазных проводников. ELCUT может с успехом использоваться для анализа инженерных систем с разных точек зрения – магнитной, электрической, тепловой, прочностной. Эти взаимосвязанные виды анализа могут быть автоматизированы для конкретной технической системы.
Пример представляет из себя Word-документ со встроенными макросами. Документ содержит результаты анализа, основывающегося на заданных исходных параметрах. Содержащиеся в нем таблицы, картинки и графики сформированы в результате автоматического расчета профессиональной версией ELCUT. Управление ELCUT происходит через объектную модель.
Таблица 1. Геометрические размеры проводников.
| Сечение фазного провода | 120 | мм² |
| Сечение нулевого провода | 35 | мм² |
| Радиус скругления проводника (R) | 2 | мм |
Таблица 2. Геометрические параметры изоляции.
| Толщина фазовой изоляции | 2 | мм |
| Толщина внутреннего слоя изоляции кабеля | 1 | мм |
| Толщина стальной ленты | 1 | мм |
| Толщина внешнего слоя изоляции кабеля | 3 | мм |
Таблица 3. Точность расчета.
| Точность вычисления площади | 0.001 | мм². |
Таблица 4. Электрическая нагрузка.
| Амплитуда фазного тока | 200 | A. |
| Амплитуда фазного напряжения | 6500 | В |
| Частота тока | 50 | Гц |
| Фазовый угол тока | 0 | град |
Таблица 5. Физические свойства проводника.
| Относительная магнитная проницаемость | 1 | |
| Электрическая проводимость | 36000000 | См/м |
| Теплопроводность | 140 | Вт/К•м |
| Модуль Юнга | 6.9e+10 | Н/м² |
| Коэффициент Пуассона | 0.33 | |
| Коэффициент теплового расширения | 2.33e-5 | 1/K |
| Плотность материала | 2700 | кг/м³ |
Таблица 6. Физические свойства стального экрана.
| Относительная магнитная проницаемость | 1000 | |
| Электрическая проводимость | 6000000 | См/м |
| Теплопроводность | 85 | Вт/К•м |
| Модуль Юнга | 2e+11 | Н/м² |
| Коэффициент Пуассона | 0.3 | |
| Коэффициент теплового расширения | 0.000012 | 1/K |
| Плотность материала | 7870 | кг/м³ |
Таблица 7. Физические свойства изоляции.
| Проводниковая | Внутренняя | Внешняя | |
| Относительная магнитная проницаемость | 1 | 1 | 1 |
| Электрическая проводимость, См/м | 0 | 0 | 0 |
| Диэлектрическая проницаемость | 2.5 | 2.5 | 2.5 |
| Теплопроводность, Вт/К•м | 0.04 | 0.04 | 0.04 |
| Модуль Юнга, Н/м² | 10000000 | 10000000 | 10000000 |
| Коэффициент Пуассона | 0.3 | 0.3 | 0.3 |
| Коэффициент теплового расширения, 1/K | 0.0001 | 0.0001 | 0.0001 |
| Плотность материала, кг/м³ | 900 | 900 | 1050 |
Таблица 8 представляет результаты вычисления геометрических характеристик кабеля по введенным исходным данным.
Внешний диаметр кабеля рассчитывается с учетом геометрических размеров проводников и изоляции, введенных в таблицах 1 и 2. Для расчета плотности и погонной массы используются вычисленные площади сечений и плотности материалов.
Таблица 8. Физические параметры кабеля.
| Внешний диаметр кабеля | 4.28e+01 | мм |
| Вес (на метр длины) | 2.74e+00 | кг |
| Средняя плотность кабеля | 1.90e+03 | кг/м² |
Расчет электростатического поля выполняется для определения собственных и взаимных частичных емкостей проводников. Результаты вычислений сведены в таблицу "Емкость проводников" (см. ниже). Значения емкости вычисляются в ходе анализа решения электростатических задач с использованием следующего подхода:
Каждой строке таблицы соответствует решение одной задачи ELCUT. В каждой такой задаче одному из проводников сообщается единичный заряд. После решения на всех проводниках измеряется наведенный потенциал, и частичные емкости проводников вычисляются по формуле:
Cij = Qi / Uj,
где Qi – заданный заряд на проводнике (i – номер строки в таблице),
Uj – наведенный потенциал на этом и других проводниках.
Собственная емкость проводника вычисляется как отношение его заряда к наведенному на нем самом потенциалу.
Таблица 9. Емкость проводников, Ф
| Проводник 1 | Проводник 2 | Проводник 3 | Нулевой провод | |
| Проводник 1 | 2.53e-10 | 1.02e-09 | 1.95e-09 | 8.43e-10 |
| Проводник 2 | 1.02e-09 | 2.67e-10 | 1.02e-09 | 1.88e-09 |
| Проводник 3 | 1.95e-09 | 1.02e-09 | 2.53e-10 | 8.42e-10 |
| Нулевой провод | 8.43e-10 | 1.88e-09 | 8.42e-10 | 1.28e-10 |
Результаты расчета индуктивностей приведены в таблице 10. Мгновенные значения токов в фазных проводниках задаются в соответствии с фазовым углом, заданным в таблице 4. Значения в левой половине таблицы (колонки 2-5) вычислены для постоянного тока, а в правой половине (колонки 6-9) – для переменного тока заданной частоты (по умолчанию 50 Гц). Для вычисления взаимных и собственных индуктивностей использовался подход, основанный на потокосцеплениях: Lij = Fj / Ii
Таблица 10. Индуктивности проводников на постоянном и переменном токе.
| постоянный ток | переменный ток | |||||||
| Пров.1 | Пров.2 | Пров.3 | Нуль. пров | Пров.1 | Пров.2 | Пров.3 | Нуль. пров | |
| Провод 1 | 1.15e-05 | 1.12e-05 | 1.11e-05 | 1.13e-05 | 6.17e-06 | 5.99e-06 | 5.94e-06 | 6.02e-06 |
| Провод 2 | 1.12e-05 | 1.15e-05 | 1.12e-05 | 1.11e-05 | 5.99e-06 | 6.17e-06 | 5.99e-06 | 5.93e-06 |
| Провод 3 | 1.11e-05 | 1.12e-05 | 1.15e-05 | 1.13e-05 | 5.94e-06 | 5.99e-06 | 6.17e-06 | 6.02e-06 |
| Нулевой провод | 3.89e-10 | 3.84e-10 | 3.89e-10 | 4.04e-10 | 6.02e-06 | 5.93e-06 | 6.02e-06 | 6.27e-06 |
Импедансы отдельных проводников и соответствующие им активные сопротивления на постоянном токе сведены в таблицу 11.
На постоянном токе активное сопротивление проводника легко вычисляется через геометрические размеры сечения и электропроводность материала как:
R = ρ · l / S,
где ρ - удельное сопротивление проводника,
S – площадь поперечного сечения,
l – длина (= 1 м)
Мощность джоулевых потерь на постоянном токе вычисляется как:
P = IA² · R,
где IA действующее значение тока в проводнике и R - его активное сопротивление.
Импеданс проводника на переменном токе вычисляется на основе закона Ома как отношение комплексного значения напряжения, приложенного к концам проводника, к комплексному значению полного тока в нем. Действительная часть этого отношения представляет собой активное сопротивление проводника на переменном токе (с учетом эффекта вытеснения и эффекта близости), а мнимая часть – индуктивное сопротивление. Мощность джоулевых потерь в проводнике на переменном токе вычисляется внутри ELCUT по формуле:
P = ò j²ρ ds,
где j - плотность тока, а интегрирование выполняется по сечению проводника.
Таблица 11. Импеданс проводников.
| Постоянный ток | Переменный ток | ||||
| Фазный провод | Нулевой провод | Пров. 1 | Пров. 2 | Пров. 3 | |
| Импеданс, Ом | 2.31e-04 | 7.94e-04 | 2.40e-04 | 2.55e-04 | 2.80e-04 |
| Активное сопротивление, Ом | 2.31e-04 | 7.94e-04 | 2.15e-04 | 2.37e-04 | 2.59e-04 |
| Реактивное сопротивление, Ом | 0.00e+00 | 0.00e+00 | 1.08e-04 | 9.41e-05 | 1.06e-04 |
| Мощность потерь, Вт | 4.63e+00 | 0.00e+00 | 4.71e+00 | 4.74e+00 | 4.71e+00 |
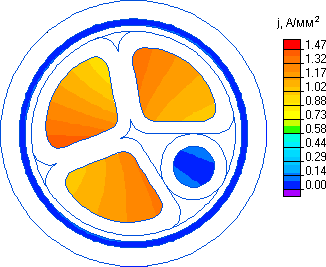
Распределение плотности тока по сечению проводников, вычисленное в задаче магнитного поля переменных токов, передается в качестве источника тепла в задачу расчета температурного поля.
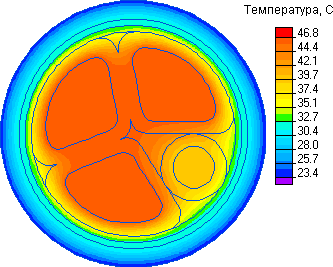
Результаты теплового расчета приводятся в таблице 12. Это средняя температура на наружной поверхности кабеля и поток тепла с этой поверхности в окружающую среду, а также средние значения температуры по сечению каждого из проводников. Приведенные в таблице значения температур вычислены в предположении, что температура окружающей среды = 20°C.
Таблица 12. Тепловые параметры кабеля.
| Средняя температура внешней поверхности кабеля | 23.5 | °C | |||
| Поток тепла в окружающее пространство | 14.2 | Вт | |||
| Средняя температура проводника, °C | |||||
| Провод 1 | Провод 2 | Провод 3 | Нулевой провод | ||
| 4.59e+01 | 4.68e+01 | 4.59e+01 | 3.93e+01 | ||
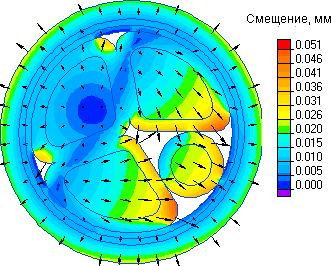
Анализ упруго-деформированного напряженного состояния элементов кабеля выполняется с учетом его теплового состояния, рассчитанного ранее. Также принимаются во внимание силы магнитного взаимодействия проводников друг с другом, которые рассчитаны при расчете магнитного поля переменных токов. Механические напряжения в элементах кабеля развиваются вследствие термических деформаций и магнитных сил. Результаты расчета приведены в таблице 13.
Таблица 13. Механические характеристики.
| Наибольшее перемещение | 5.14e-02 | мм |
| Максимальное значение критерия прочности по Мору | 8.16e+07 | Н/м² |
При анализе электрической прочности изоляционных систем кабеля, необходимо знать максимальное значение напряженности электрического поля.
Таблица 14. Напряженность электрического поля.
| Максимальная напряженность в сечении | 8.78e+03 | В/м |
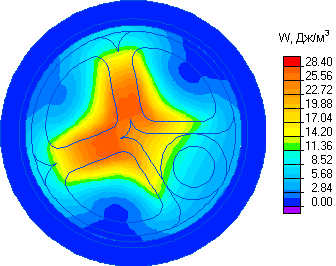
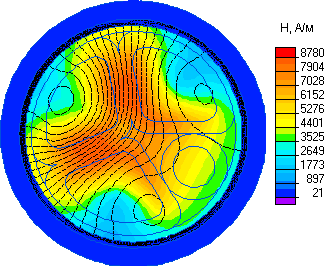
Ниже приводятся картины распределения напряженности электрического поля, плотности тока (с учетом вихревых токов), плотности энергии магнитного поля, мгновенного значения магнитной индукции на переменном токе, распределения температуры по сечению проводника и механического перемещения под действием термических деформаций и магнитных усилий.