Главная >> Применение >> Типовые примеры >>

Закон Ампера

закон Ампера, сила Ампера на переменном токе, проводник с током магнитная сила, магнитное поле, магнитная сила между двумя проводниками с током, магнитная сила между двумя проводниками

Пример посвящен сравнению значения силы взаимодействия двух тонких проводов с токами, посчитанной по формуле Ампера и в ELCUT для трёх формулировок: магнитостатики, переменного магнитного поля и нестационарного магнитного поля.

Геометрия

Дано
I = 1 А - ток в каждом из проводов;
f = 50 Гц - частота тока в задачах магнитного поля переменных токов и в нестационарной магнитной задаче;
r = 1 м - расстояние между проводами.

Задание
Рассчитать пондеромоторную силу (на метр длины провода), действующую на провода и сравнить результат с формулой Ампера.

Решение
Токи в модели задаются линейные. Так модель будет точно соответствовать постановке, описываемой формулой Ампера.
В задаче магнитного поля переменных токов задано амплитудное значение тока √2·I.
В нестационарной задаче ток задан формулой I(t) = √2·I · sin(2·180·50·t).

Согласно закону Ампера* сила взаимодействия между параллельными проводами с током составляет:
F = 2·(μ₀/4π) · I·I / r [Н/м]

Результаты:
Закон Ампера: F = 2·(μ₀/4π) · 1·1/ 1 = 2·10^-7 [Н/м]

Магнитостатика:

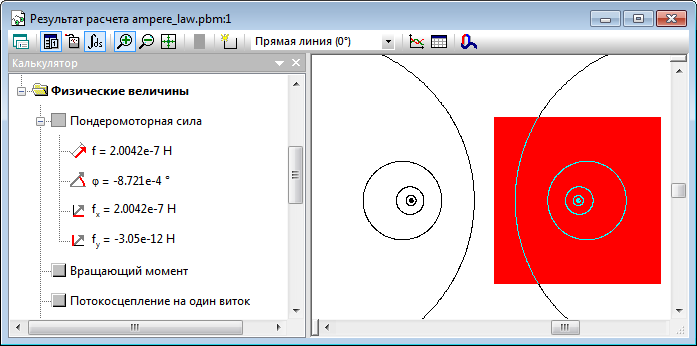
Переменное магнитное поле:

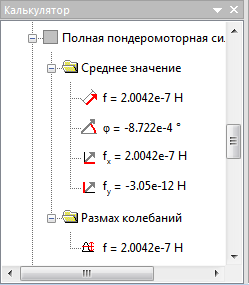
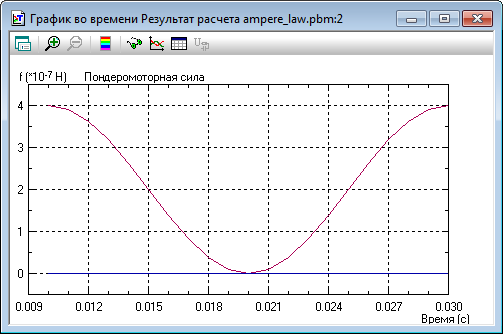
Нестационарное магнитное поле:

Время	Ток	Сила
0.01 с	2 A	4.0092·10-7 Н/м
0.015 с	1 A	2.0046·10-7 Н/м
0.02 с	0 A	6.255·10-22 Н/м

	F, *10-7 Н/м	Погрешность
Формула Ампера	2.000	-
Магнитостатика	2.0042	0.2%
Переменное магнитное поле	2.0042	0.2%
Нестационарное магнитное поле	2.0046	0.2%

*Википедия: Закон Ампера.

• Видео: Закон Ампера
  
• Скачать файлы задачи