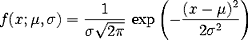
Среднее значение - это среднее арифметическое значение результатов испытаний.
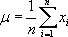
Для статистического анализа, как правило, это величина близка к номинальному значению.
Стандартное отклонение - это среднеквадратичное значение для отклонений рассчитанных значений от среднего значения.
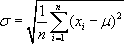
Эту величину можно рассматривать как оценку того, насколько в среднем значения отклоняются от среднего. Во многих случаях удобно также использовать величину 3*σ, как оценку максимального отклонения значений от среднего. См. подробнее Роль величины 3*Sigma для нормального распределения.
Нормальное распределение - это распределение случайной величины, плотность которого задается функцией:
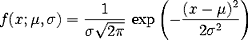
где μ - среднее значение, а σ - стандартное отклонение.
Нормальное распределение очень часто встречается при исследовании физических явлений и решении инженерных задач. Как правило, распределение будет нормальным во всех случаях, когда величина определяется большим количеством независимых случайных факторов, причем вклады этих факторов складываются.
В статистическом анализе предположения о нормальном распределении используются и при генерации случайных изменений, и при оценке распределения результатов.
Про генерации случайных изменений, величина изменения предполагается распределенной нормально.
Для распределения результатов мы не можем быть уверены в том, что оно нормальное. Но во многих случаях, особенно если вы задаем большое количество исходных допусков, распределение будет близко к нормальному.
Если это не так, то, как правило, результаты статистического анализа все равно могут быть использованы, но при этом точность статистических оценок будет ниже.
Для оценки нормально распределенной случайной величины часто используют значение 3*у. Причина этого в том, что большинство (99.7%) значений нормального распределения лежит в интервале от μ - 3*σ до μ + 3*σ. (Это хорошо видно на графике - в точках μ - 3*σ и μ + 3*σ кривая нормального распределения практически сливается с осью X).
Во многих случаях мы может рассматривать 3*σ, как хорошую оценку максимального отклонения .
В подсистеме статистического анализа значение 3*σ используется при задании допусков и и при оценке результатов.
Для допуска 3*σ - это то значение, которое мы указываем его описании.
Например, пусть для некоторого свойства мы указали, что оно может меняться с допуском 1%. Это означает, что будет использоваться нормальное распределение с σ = 0.33%. Тем самым, практически все случайные отклонения будут попадать в интервал +-1%
Кроме этого, 3*σ используется при расчете максимального отклонения и верхнего и нижнего пределов:
Таким образом, для распределения, близкого к нормальному, верхний и нижний пределы задают интервал, в который попадут практически все результаты испытаний. Если распределение далеко от нормального, мы не можем этого гарантировать. Тем не менее, как правило 3*σ - это хорошая оценка и для других видов распределения.
Как правило, можно использовать следующие оценки:
В результате можно посоветовать использовать такую схему исследования:
См.также
Статистический анализ -
обзор основных понятий и возможностей