Эллипсоид из диэлектрика в однородном электрическом поле

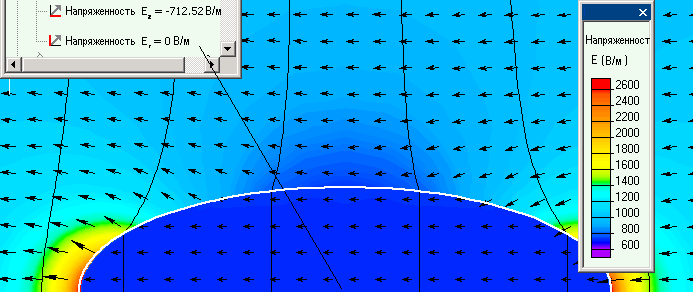
Эллипсоид из диэлектрика помещен в однородное электрическое поле. Вектор напряженности внешнего поля сонаправлен с главной осью эллипсоида.

Тип задачи: электростатика.

Геометрия: Осесимметричная / 3D импорт.

Дано:
Длина вдоль оси Z: dz = 0.05 м.
Длина вдоль осей X и Y: dx = dy = 0.02 м.
Относительная диэлектрическая проницаемость воздуха ε₀ = 1,
Относительная диэлектрическая проницаемость диэлектрика ε_r = 4,
Напряженность внешнего поля E_ext = 1 кВ/м.

Задание:
Рассчитать распределение электрического поля внутри эллипсоида.

Решение:
Аналитическое решение для 2D-задачи (вектор внешнего поля E_внеш направлен вдоль оси Z):
Напряженность электрического поля внутри эллипса E_z = E_внеш / (1+(ε_r - 1)·n_z), где
     коэффициент деполяризации n_z = (1 - e²)/e³ * (Artanh(e) - e),
     эксцентриситет эллипса e = sqrt(1 - dx²/dz²).

В том случае, когда вектор внешнего поля E_внеш сонаправлен с одной из осей эллипсоида, геометрическая модель может быть построена как осесимметрическая 2D-модель, представленная в ELCUT в виде верхней половины поперечного сечения эллипсоида (в общем случае задача является 3D-задачей).

Результаты:
Эксцентриситет эллипса e = sqrt(1 - 0.02²/0.05²) = 0.917,
Коэффициент деполяризации n_z = (1 - 0.917²)/0.917³ * (Artanh(0.917) - 0.917) = 0.135.
Напряженность однородного электрического поля внутри эллипсоида (аналитическое решение):
E_z = 1000 / (1 + (4 - 1)·0.135) = 711 В/м.

ELCUT 2D: E_z = 712 В/м.

ELCUT 3D: E_z = 711 В/м.

Распределение электрического поля внутри и снаружи эллипсоида (2D- и 3D-задачи):

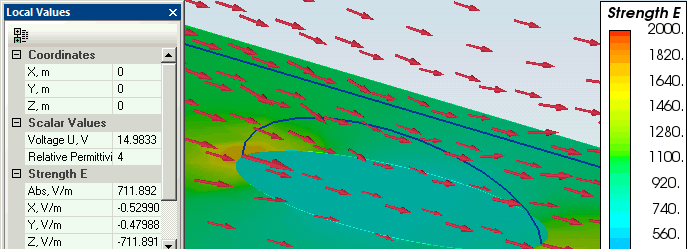
См. задачу dielectric_ellipsoid.pbm в папке с примерами.