{δ} =
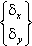
- в плоских задачах;
{δ} =
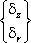
- в осесимметричных задачах.
Комплекс ELCUT может решать задачи теории упругости в постановках плоских напряжений, плоских деформаций и осесимметричного напряженного состояния с изотропными или ортотропными свойствами материалов. Задача плоских напряжений подходит для анализа структур, тонких по глубине, которые нагружены в плоскости модели. Напряжение в направлении, нормальном к плоскости модели, предполагается отсутствующим. Задача плоских деформаций предполагает отсутствие деформаций вне плоскости модели. Эта задача подходит для моделирования объектов с весьма большой толщиной в направлении, нормальном к плоскости модели.
Во всех постановках поле перемещений однозначно определяется двумя компонентами вектора перемещений δ в каждой точке:
|
{δ} = |

|
- в плоских задачах; |
|
{δ} = |

|
- в осесимметричных задачах. |
В обеих плоских постановках рассматривается только по три компоненты деформаций и напряжений. Деформация связана с перемещением соотношением:
|
{ε} = |
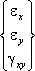
|
= |
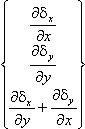
|
. |
Соответствующее ей напряжение выражается как
|
{σ} = |
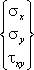
|
. |
В осесимметричном случае радиальное перемещение приводит к деформации εθ в направлении, перпендикулярном плоскости модели, поэтому выражение для полной деформации имеет вид:
|
{ε} = |
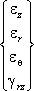
|
= |
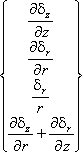
|
. |
Соответствующие компоненты напряжений:
|
{σ} = |
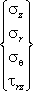
|
. |
Уравнения статического равновесия для плоских задач имеют следующий вид:
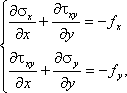
а для осесимметричных задач:
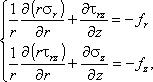
где fx, fy и fz, fr - компоненты вектора плотности объемной силы.
Соотношение между напряжениями и деформациями при упругом поведении материалов выражается зависимостью:
{σ} = [D]({ε} - {ε0}),
где D - матрица упругости, и ε0 - начальная термическая деформация, вызванная перепадом температур. Вид матрицы зависит от применяемой постановки.
Матрица упругости для плоского напряженного состояния (изотропный материал):
|
[D] = |
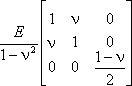
|
. |
Плоские напряжения, ортотропный материал:
|
[D] = |
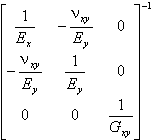
|
. |
Плоские деформации в изотропном материале:
|
[D] = |
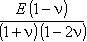
|
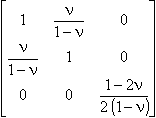
|
. |
Плоские деформации в ортотропном материале:
|
[D] = |
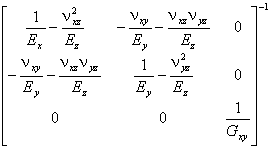
|
. |
Осесимметричная задача, изотропный материал:
|
[D] = |
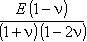
|

|
. |
осесимметричная задача, ортотропный материал:
|
[D] = |
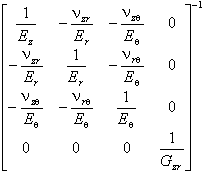
|
. |
В этих формулах E - модуль Юнга в изотропном случае;
Ex, Ey, Ez, Er, и Eθ модули Юнга в направлении соответствующих осей в материале с ортотропными свойствами;
ν - коэффициент Пуассона изотропного материала;
νyx, νzx, νzy, νrz, νθz, νθr - коэффициенты Пуассона для указанных пар осей в ортотропном случае;
Gxy или Gzr - модуль сдвига.