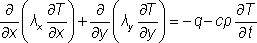
- в плоском случае;
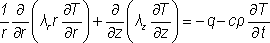
- в осесимметричном случае;
ELCUT позволяет решать задачи теплопередачи в линейной и нелинейной постановках. При решении тепловых задач используется уравнение теплопроводности в одном из видов:
Для линейных задач:
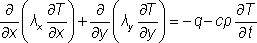
|
- в плоском случае; |
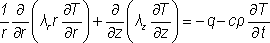
|
- в осесимметричном случае; |
Для нелинейных задач:
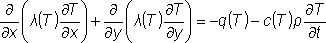
|
- в плоском случае; |
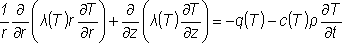
|
- в осесимметричном случае; |
где:
T - температура;
t - время;
λx(y,r,z) - компоненты тензора теплопроводности (в линейной постановке);
λ(T) - теплопроводность как функция температуры, представленная кубическим сплайном (анизотропия не поддерживается в нелинейной постановке);
q(T) - удельная мощность тепловыделения; в линейной постановке - константа, в нелинейной постановке - задаваемая кубическим сплайном функция температуры;
c(T) - удельная теплоемкость, в нелинейном случае это функция температуры, аппроксимированная кубическими сплайнами;
ρ - плотность.
Все параметры уравнений в линейной постановке постоянны в пределах каждого блока модели.
Постановка задачи распределения температурного поля в тонких пластинах весьма похожа на формулировку плоско-параллельной задачи и мы не будем обсуждать её отдельно.