Примеры

ELCUT позволяет в некоторых случаях (например, при задании граничных условий) использовать формулы. Синтаксис формул очень прост. Здесь же приводятся некоторые примеры формул, которые должны помочь вам в создании ваших собственных выражений. В левом столбце приводятся математические формулы, а в правом - соответствующая запись, пригодная для использования в ELCUT.

Функция	График	Запись в ELCUT
100·t		100*t
t·(1 - t)·(2 - t)		t*(1-t)*(2-t)
2·t2 - t - 3		2*t^2 - t - 3
e-t 2/2		exp(-t^2 / 2)
log2t		log(t) / log(2)
sin t + cos t		sin(t) + cos(t)
200·sin(18000·t + 240)		200*sin(18000*t+240)
2t		2^t
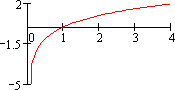
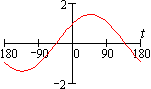
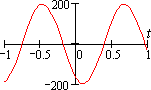
tg t 2.4·10-8		tan(t / 2.4e-8)
|2π·t|		abs(2*pi*t)
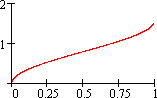
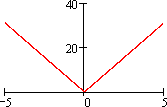
t, при t < 0.5 1-t, при t ≥ 0.5		t*step(0.5-t) + (1-t)*step(t-0.5)
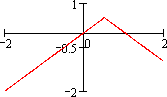
0, при t < 0 t, при 0 ≤ t < 0.5 1-t, при 0.5 ≤ t < 1 0, при t ≥ 1		t*impulse(t,0,0.5) + (1-t)*impulse(t,0.5,1)
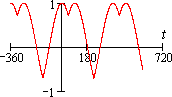
sin(t), при sin(t) > cos(t) cos(t), при sin(t) ≤ cos(t)		max(sin(t), cos(t))
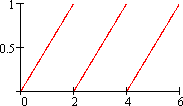
t/2, при 0 ≤ t < 2 периодична с периодом 2		saw(t, 2)
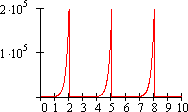
10·e5t, при 0 ≤ t < 2 10, при 2 ≤ t < 3 периодична с периодом 3		10 * exp(5 * saw(t,2,1)) Периодичность функции достигается заменой аргумента t на функцию saw ("пила").
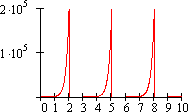
10·e5t, при 0 ≤ t < 2 0, при 2 ≤ t < 3 периодична с периодом 3		10 * exp(5 * saw(t,3)) * impulse(saw(t,3), 0, 2/3) Нулевое значение определяется функцией impulse ("импульс"). Периодичность функции достигается заменой аргумента t на функцию saw ("пила").
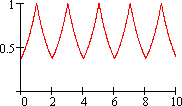
et-1, при 0 ≤ t < 1 e1-t, при 1 ≤ t < 2 периодична с периодом 2		exp(saw(t,1,1)-1) + exp(saw(2-t,1,1)-1) - exp(-1) Функцию можно представить как сумму двух периодических функций. Периодичность функции достигается заменой аргумента t на функцию saw ("пила").
Симметричный меандр		sign(sin(t))
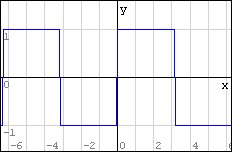
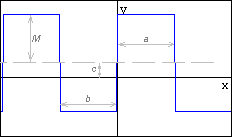
Несимметричный меандр		2*M*sign(saw(t,a,b)) - M + c Периодичность функции достигается заменой аргумента t на функцию saw ("пила") c длиной сигнала a и периодом (a+b).
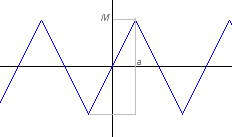
Треугольная функция		2*M*saw(t+a,2*a,2*a) + 2*M*saw(-t-a,2*a,2*a) - M Функции может быть представлена, как сумма двух периодических функций saw ("пила").