Синусоидальное напряжение приложено к катушке со стальным сердечником.
Тип задачи:
Осесимметричная задача нестационарного магнитного поля с присоединенной электрической цепью.
Геометрия:
Ввиду симметрии задачи мы можем оставить в расчетной области только правую половину катушки (показана верхней половиной ее поперечного сечения). Поэтому значения параметров элементов электрической цепи должны быть уменьшены вдвое против их номинального значения.
Дано:
Магнитная проницаемость стального сердечника μ - нелинейная;
Электропроводность стального сердечника γ = 10 000 000 См/м;
Магнитная проницаемость катушки μ = 1;
Электропроводность катушки (медь) γ = 56 000 000 См/м;
Число витков катушки w = 120;
Амплитуда приложенного напряжения U = 10*sqrt(2) В;
Частота f = 50 Гц.
Задача:
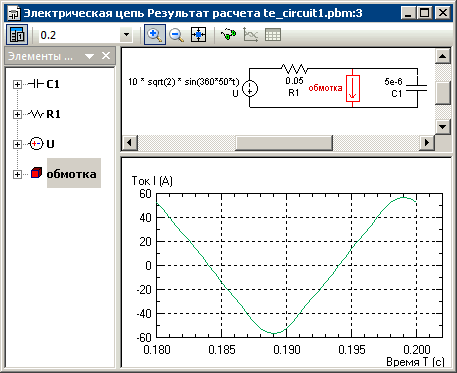
Рассчитать ток в обмотке в зависимости от времени.
Решение:
Период синусоидального тока составляет T = 1 / f = 0.02 с. Выберем шаг по времени равным 0.0005 с. чтобы гарантировать гладкую кривую во времени. Финальное время 0.2 с включает 10 периодов, что достаточно для затухания переходной составляющей тока. Чтобы сократить размер файла решения задачи, запросим вывод результатов только в течение последнего периода (начиная с момента времени 0.18 с).
Результат:

Если разложить кривую тока в ряд Фурье, то можно видеть:
I(t) = 59.6·cos(t·2π/T - 166°)
См. задачуTECircuit1.pbm в папке с примерами.