Бегущее магнитное поле, создаваемое индуктором насоса, наводит вихревые токи в расплавленном металле. Величина этих токов зависит от сопротивления металла, которое в свою очередь зависит от его температуры. Рассчитать мощность насоса, как функцию температуры металла.
Тип задачи:
Осесимметричная задача магнитного поля переменных токов.
Геометрия:
В виду симметрии рассматриваемой геометрии в модели представлена только верхняя её часть.
Дано:
Магнитная проницаемость стального сердечника μ = 200;
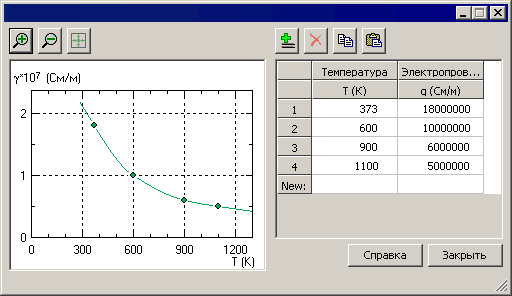
Проводимость расплава γ - зависит от температуры;
Плотность тока в обмотке j = 6 A/мм2;
Частота тока f = 50 Гц.

Задача:
Рассчитать мощность насоса как функцию температуры металла.
Решение:
Поскольку индуцируемые токи быстро затухают вдоль оси Z, можно рассматривать сравнительно небольшую длину модели - 400 мм.
Зависимость сопротивления от температуры задана для блока "расплав". Задача решается для нескольких значений температуры расплава.
Для вычисляется силы строится контур вокруг блока "расплав" и вычисляется интеграл "Механическая сила".
Результаты:
| Температура, °C | Сила, H | Давление, Па |
| 100 | 41 | 14 500 |
| 200 | 30 | 10 500 |
| 600 | 23 | 8 100 |
| 900 | 18 | 6 500 |
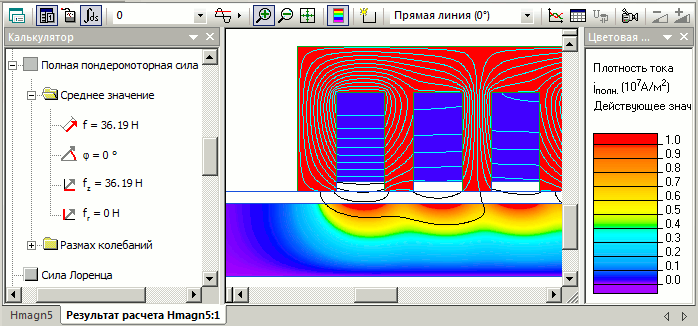
Смотрите задачу HMagn5.pbm в папке с примерами.