Dirich1: Проводящий цилиндр во вращающемся магнитном поле

Тип задачи:
Плоско-параллельная задача расчета нестационарного магнитного поля.

Геометрия:

Дано:

Относительная магнитная проницаемость воздуха и проводника μ = 1;
Электропроводность проводника γ = 6.3·10⁷ См/м;
Величина индукции внешнего поля B₀ = 1 Тл;
Число полюсов 2p = 6;
Частота тока f = 50 Гц.

Решение:
Чтобы задать вращающееся магнитное поле на внешней границе области, B_n = B₀ sin (ωt - pφ), приложим граничное условие Дирихле вида: A = cos (18000*t - 3*atan2 (y/x)) / 60

Коэффициент A₀ = 1/60 получается из выражения

B_n = (1/r)(∂A/∂φ) = A₀p·sin(ωt - pφ) / r

и

A₀ = B₀·r/p

Благодаря периодичности поля используем только половину модели и задаем периодическое граничное условие A₁ = -A₂ на плоскости разреза. В действительности, достаточно использовать сектор в 60°. Время интегрирования 0.05 с (около 2.5 периодов). Шаг интегрирования по времени выбирается автоматически.

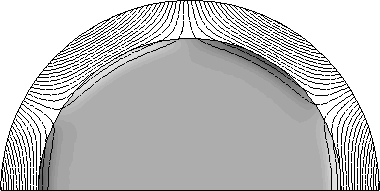
Результаты:
t = 0.0002 с:

t = 0.048 с:

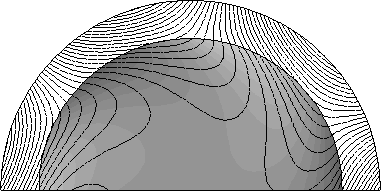
t = 0.05 с:

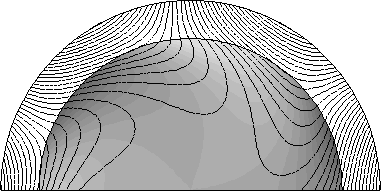
См. задачу Dirich1.pbm в папке с примерами.