Переменный ток в плоском конденсаторе
Тип задачи:
Плоско-параллельная задача расчета электрического поля переменных токов.
Геометрия:
Вследствие симметрии рассматриваем небольшую часть высотой 1 мм. Длина конденсатора в направлении оси z составляет L = 10 мм.
Дано:
Относительная диэлектрическая проницаемость диэлектрика ε = 10.
Электропроводность диэлектрика γ = 10-8 См/м;
Напряжение U = 5 В,
Частота f = 50 Гц.
Задача:
Найти ток и тангенс угла потерь tg(δ) плоского конденсатора с неидеальным диэлектриком внутри.
Решение:
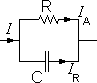
Конденсатор с неидеальным диэлектриком может быть заменен электрической схемой с идеальным конденсатором C и сопротивлением R, соединенными параллельно.

Ёмкость плоского конденсатора вычисляется по формуле
C = εε0S/d, где S - площадь поверхности пластины, S = h·l.
Сопротивление диэлектрика вычисляется по формуле
R = ρ·d/S.
Ток I имеет две компоненты: активную IA и реактивную IR. Для параллельного соединения
IA = U / R, IR = U / XC.
tg(δ) = |PA / PR| = |U·IA / U·IR| = |IA / IR|
Результаты:
S = 100 мм2.
R = (1/10-8)·0.1e-3/100e-6 = 109 Ом.
C = 10·8.854e-12·100e-6/0.1e-3 = 8.854·10-11 Ф.
XC = 1 / 2·3.1416·50·8.854·10-11 = 0.3595·109 Ом.
IA = 5 / 109 = 5·10-9 A
IR = 5 / 0.3595·109 = 13.908·10-9 A
tg(δ) = 5·10-9 / 13.908·10-9 = 0.36
| ELCUT | Теория | |
| IA, A | 5·10-9 | 5·10-9 |
| IR, A | 13.908·10-9 | 13.908·10-9 |
| tg(δ) | 0.36 | 0.36 |